Department of Physics, U-46, University of Connecticut, Storrs, CT 06269-3046
s time scale, in reasonable agreement with trajectory simulations.The ability to follow microscopic systems in real time has become an
increasingly important factor in providing information on the system dynamics.
Since the relevant time scale is typically quite short (e.g., 
s for molecules), extremely fast probes (e.g., ultrafast lasers) are usually
required. However, with ultracold atoms (e.g., T<1 mK), the time scale
for interactions can be much longer. Obviously, the low atomic velocity
is one contributing factor. The other, less obvious aspect is the fact
that extremely long-range interatomic potentials can dominate the interactions
between these nearly stationary atoms, leading to a greatly increased length
scale. We report here our observations of the temporal dynamics of collisions
between ultracold atoms occuring on the submicrosecond time scale. Our
measurements can be viewed as a stroboscopic following of these very slow
collisions in real time.
A great deal of related work has been done on much faster time scales. Transition-state dynamics and chemical reactions have been probed using femtosecond lasers [1, 2] and bound molecular wave packets have been created and followed in real time using femtosecond pump-probe techniques [3, 4] or time- and frequency-resolved spontaneous emission [5]. Trajectories of continuum wave packets for dissociating molecules (half collisions) have been followed with picosecond resolution via Coulomb explosion [6], and photoassociation, the formation of bound molecules using light, has been observed to occur on the femtosecond time scale at room temperature [7]. In atomic collision studies at room temperature, collision times on the order of a picosecond were inferred from the dependence of the collision rate on laser pulse duration [8].
There has been some limited work performed on slower time scales. Subnanosecond
wavepacket dynamics of ultracold photoassociative ionization has been discussed
[9]
and time-dependent studies of cold-atom photoassociation have revealed
a long-lived ( 
s) shape resonance in the scattering of cold ground-state atoms [10].
Also, resonant energy-transfer collisions between velocity-selected Rydberg
atoms have been observed to take place on the microsecond time scale [11].
In the present work, we investigate the temporal evolution of collisions
involving laser-excited ultracold atoms. This brings into play the extremely
long-range ( 
) resonant dipole interaction between a ground- and excited-state atom. At low
temperatures, this potential energy can greatly exceed the typical kinetic
energy even for internuclear separations R>100 nm. Combining this extensive
length scale with the low initial atomic velocities (v 
10 cm/s), we find a collisional time scale in the
s range. This is to be contrasted with collisions at room temperature (v 
m/s) where the atomic trajectories are not affected until R<1 nm, yielding
typical collision times on the order of 
s. Obviously, in the ultracold case, collision times can exceed the excited-state
lifetime ( 
s), meaning that spontaneous decay can occur during the course of the collision.
This fact, coupled with the long range of the interactions and the low
atomic kinetic energies, has led to a great deal of interest in the area
of ultracold collisions [12,
13,
14,
15].
Understanding these collisions is also important because they can be a
density-limiting mechanism for laser-cooled atomic samples which are used
in various applications (e.g., Bose-Einstein condensation).
In our experiment, we use a pump-probe arrangement with two separate
lasers to follow the collisional trajectories in real time. Our signal
is based on the flux enhancement effect which we have recently observed
in steady state [16].
As shown in Fig. 1a,
one laser (the trap laser) is tuned close to the atomic resonance (detuned
by 
where 
(5.89 MHz) is the atomic decay rate), thereby exciting atom pairs to the
attractive 
potential at very long range (Condon radius 
). Since the atoms are initially moving so slowly, and their acceleration
is small, spontaneous decay occurs before the atoms approach closely enough
for an inelastic trap loss process (e. g., radiative escape (RE) or a fine-structure
change ( 
)) to occur [17].
In other words, the excitation does not survive to short range. Although
no observable trap loss collision occurs, the trajectories are significantly
affected. In particular, the deflections result in an enhanced ground-state
collisional flux available for the second (probe) laser which is tuned
farther below the atomic resonance ( 
) and capable of exciting atom pairs at shorter range ( 
). Atom pairs excited by the probe laser are quickly accelerated by the
steeper attractive potential and are much more likely to undergo an inelastic
trap loss collision. However, the rate of collisions induced by this laser
alone is relatively low, because its smaller 
results in less collisional flux intercepted. The two lasers, acting in
concert, yield a relatively high rate of collisions, i.e., the trap laser
provides an enhanced flux which the probe laser causes to collide efficiently.
The key point of the present paper is that this flux enhancement effect
takes place on a rather long time scale, i.e., the atoms travel slowly
from 
to
. We observe this by pulsing the two excitations and measuring the enhanced
collision rate as a function of delay between the pulses.
We have performed semiclassical numerical calculations of the distribution
of collision times for the parameters of our experiment. In these simulations,
we calculate the collision time (i.e., the time to travel from
to
) for an atom pair with initial impact parameter 
and relative velocity 
. The atom pair is assumed to interact with the trap laser only at
, i.e., off-resonant excitation is ignored. The excitation process is calculated
as a Landau-Zener probability using the atomic Rabi rate divided by 
(to account for directional averaging [16,
18]).
The classical trajectory (Figure 1b)
of the excited atoms under the influence of the attractive potential is
followed until spontaneous emission at time 
returns the atom pair to the ground state (5s 
5s) potential, which is assumed to be flat. Therefore, the velocity and
time of arrival at
, where the second excitation occurs, are calculated assuming a straight
line trajectory after the spontaneous decay from the first excitation.
The probability of excitation at
by the probe laser is also calculated as a Landau-Zener process. The survival
after the second (probe) excitation is not an issue. The starting radius
is sufficiently small and the attractive potential sufficiently steep that
an excited atom makes it all the way into short range, where the inelastic
trap loss process occurs, before decaying.
Trajectories will have different collision times depending on the values
of
,
, and
. Therefore we average over these parameters (weighted by their normalized
distribution functions 
and 
) to arrive at the distribution of collision times:
where
and
Here 
is the (R-dependent) molecular excited-state lifetime, M is the reduced
mass, T is temperature, and 
is the total time from
to
for a molecule that spends time
in the excited state. 
and 
are the excitation probabilities due to trap and probe lasers respectively,
using the Landau-Zener formula in the dressed-atom picture[15]. The factor 
in (1) takes account of the fact that in our experiment, we measure the
difference between inelastic collision rates with both lasers on and with
the probe laser on alone, so the effect of the probe laser alone must be
factored out of the simulation. We assume delta-function trap and probe
pulses. The hyperfine structure is ignored and detunings are referenced
to the 5s 
5p 
asymptote for 
Rb.
An example of the code used for this simulation, in C++, is found here.
The five curves in Figure 2
are plots of 
for each of the five attractive (Hund's case (c)) molecular states of the
Rb atom which are optically coupled to the ground state[17]
.
Clearly each of these states, characterized by different 
coefficients (ranging from 
for 
to 
for 
, where 
is the square of the dipole matrix element) and lifetimes (ranging from 
for 
to 
for
, where 
is the atomic lifetime), will contribute a different distribution of collision
times to the total measured. In particular, the
and 
states, which have the longest excited-state lifetimes, contribute significantly
more to the flux enhancement than the other three states and have considerably
shorter collision times. This is due to the improved survival (after the
first excitation) of these longer-lived states and the larger radial velocity
(and hence greater deflection) obtained during their longer lifetime on
the attractive excited potential. In fact, the simulations show that the
lifetime is much more important that the
coefficient in determining the distribution of collision times. Another
fact which emerges is that the energy gained as a result of the first excitation
is typically rather small, indicating that the decay does indeed occur
at long range, causing the atoms to travel most of the way from
to
in the ground state. As we would expect, simulations at higher temperatures
yield shorter average collision times. We note that the
state is coupled to the ground state only through retardation effects[17].
Its lifetime is therefore strongly dependent on R (infinite at short range),
a fact which is included in the simulations.
The experiment is performed by measuring the laser-induced collisional
decay rate of 
atoms confined in a magneto-optical trap[19]
(MOT). The trap and probe lasers are detuned by 
and 
from the 
atomic resonance at 780nm. The probe laser passes through the MOT at 
between the two radial MOT trapping beams, with a 
diameter roughly twice that of the atom cloud. The probe laser is circularly
polarized and retroreflected to create a uniform intensity 
laser field with a total intensity of 
. The trap laser intensity is fixed at 
, resulting in a very small trap-laser-induced collisional loss rate 
, due to the low-temperature suppression effect [20].
Keeping this low background 
is crucial to accurately measuring small changes,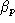 
,
induced by the probe laser. Both lasers are chopped by AOM's with a 
rise time of 30 ns. Other details of the trap parameters can be found in
[16].
The temperature of the atoms at the intensity and detuning we use was previously
[21]
measured to be 
K.
The timing scheme for the experiment is shown in Figure 3a.
The trap laser is chopped with a 
s period and a 
duty cycle. During the 5 
s cooling/trapping phase, the trap laser is on at low intensity 
to keep the atoms cooled and maintain the trap depth. During the 5
s probe phase, a more intense 
100 ns (FWHM) trap laser pulse is applied, followed, after a variable delay 
, by a 100 ns probe laser pulse. This sequence is repeated five times,
once every 1
s, during the probe phase.
To measure the increase in the trap loss collision rate constant 
, we measure it with only the trap laser on 
, then with both trap and probe lasers on 
. We then define 
. By subtracting 
, we ensure that any systematic errors produced by small changes in laser
alignment, trap laser intensity, excited state fraction or density of the
atom cloud will be reduced.
Experimental results are shown in Fig. 3b
where
is plotted as a function of pulse delay. As can be seen, there is a well-defined
peak in the time-dependent signal, characteristic of the transit time between
the two laser excitations at long- and short-range. There are essentially
no enhanced collisions until a delay of 200 ns. The curve then rises
steeply and falls off slowly for long delays. This behavior is consistent
with the predictions of the simulations (Fig. 2),
in particular the contributions of the the
and
potential curves, indicating the importance of long-lived molecular states
to the trap loss process. There is a rate of inelastic collisions which
is independent of delay, which of course are those collisions induced by
the probe laser without any enhancement by the trap laser.
It is difficult for us to quantitatively compare our measurements and
simulations because hyperfine structure and non-adiabatic effects significantly
influence evolution on the interatomic potentials near the atomic asymptotes
[22,
23].
In fact, near-resonant trap-loss collisions in general are not well understood,
although long-lived states, such as the
, are thought to play an important role [17,
24,
25].
In our case, we are mainly concerned with the attractive potentials which
converge to the 
limit. According to our simulations, most atom pairs excited by the trap
laser decay at long range, i.e., before encountering the myriad of hyperfine
curve crossings. This is true even for long-lived states, e.g., 90% of
the
excitations (which would contribute to our flux enhancement signal) decay
before reaching R=36nm (c.f. 
, 
) and thus gain less than 
of energy. This is to be compared to the 
splitting between the F' = 3 and F' = 4 excited-state hyperfine
levels. Although the Hund's case (c) labels no longer apply in this hyperfine-dominated
regime, there undoubtedly exist attractive states which are long-lived
at large R. As can be seen in comparing Figs. 2
and 3,
these potentials appear to contribute significantly to our signal.
In future experiments, measurements of collisional time evolution for different detunings of the initial excitation and for different atomic asymptotes may help sort out the roles of the various hyperfine curves. In fact, our simulations indicate that the flux enhancement factor can be larger (because of improved survival) for increased trap laser detunings. A time-dependent flux enhancement may also prove useful for investigating collisional processes which use time-resolved (e.g., ionization) detection. Better time resolution will also allow the use of enhanced flux arriving on excited as well as ground-state potentials.
In conclusion, we have demonstrated a novel technique for the study of ultracold collisions in the time domain. These time-resolved collisions yield information complementary to that obtained from photoassociative or trap loss spectra. In general, spectral information is better suited for processes occuring on fast time scales, e.g., molecular vibrations (measured by vibrational spacings) and predissociation rates (measured by linewidths). However, the spectral resolution, especially near the atomic limit, is usually not sufficient to reveal dynamics on the submicrosecond time scale, such as those responsible for the trap loss collisions we have investigated here. The present results are not only a striking demonstration of the ability to follow these slow collisions in real time, but have already yielded useful information concerning the importance of long-lived molecular states to the trap loss process.
We acknowledge technical assistance from S. Ciris and useful discussions
with E. Tiesinga regarding the effects of hyperfine structure on the long-range
molecular potentials. This work was supported in part by the Division of
Chemical Sciences, Office of Basic Energy Sciences, Office of Energy Research,
U.S. Department of Energy. S.G. acknowledges financial support from the
Connecticut Space Grant College Consortium.