 One of the major recent achievement in physics has been the ability of
cooling atomic, and more recently molecular, samples into the ultracold
temperature regime near 1 mK or less. At those low energies,
only a few partial waves contribute to scattering processes. The
leading contribution (unless forbidden by particle statistics) is
the s-wave (or ℓ = 0 partial wave) scattering, which
can be described by the scattering length
One of the major recent achievement in physics has been the ability of
cooling atomic, and more recently molecular, samples into the ultracold
temperature regime near 1 mK or less. At those low energies,
only a few partial waves contribute to scattering processes. The
leading contribution (unless forbidden by particle statistics) is
the s-wave (or ℓ = 0 partial wave) scattering, which
can be described by the scattering length
![]() ,
,
β accounts for the inelastic
processes: for purely elastic scattering, a
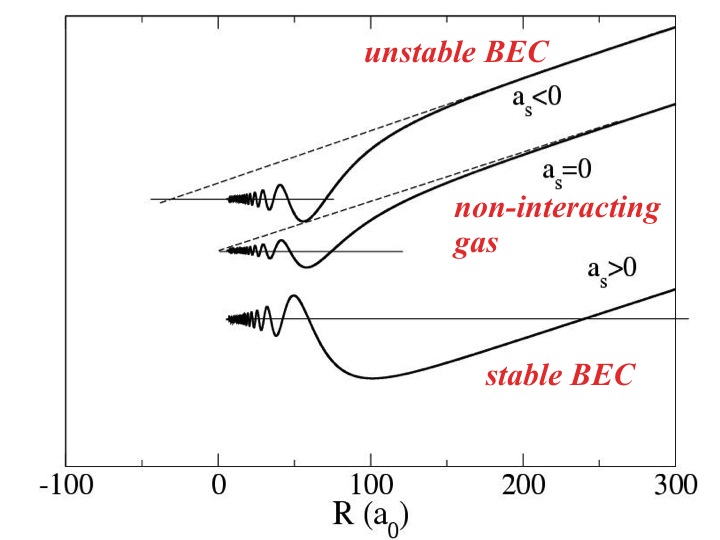
= α is real. The figure beside illustrates the concept of
scattering length as the point at which the asymptotic (dashed line)
wave function
ψ
∝
( r - a ) crosses
zero. A positive value corresponds to a repulsive interaction, a negative "length"
to an attractive interaction (leading to a stable and an unstable BEC, respectively),
and a = 0 to
a non-interacting system. In the s-wave limit, the cross sections
(the effective size of a target seen by a projectile) for
distinguishable particles can be written as
 ,
,
 As discussed in the case of degenerate gases, the scattering
length dictates the behavior of the system. It is also the
parameter governing thermalization and cooling to low
temperatures. The value of a
can be modified and tuned using external fields, as in the case
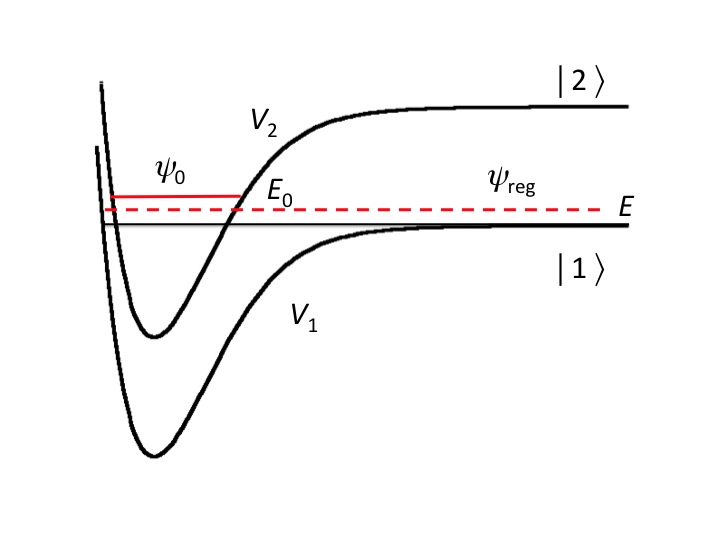
of magnetically tuned Feshbach resonances. These occur when
the energy of a bound state E0
in a closed channel coincides
with the scattering energy E (see figure beside).
The coupling between the curve V1
and V2 (e.g., due to hyperfine
and Zeeman interactions) enhances the mixing of the corresponding
wave functions
ψ0
and ψreg.
In the case of a magnetically tuned Feshbach resonance, the scattering
length can then be parametrized as
As discussed in the case of degenerate gases, the scattering
length dictates the behavior of the system. It is also the
parameter governing thermalization and cooling to low
temperatures. The value of a
can be modified and tuned using external fields, as in the case
of magnetically tuned Feshbach resonances. These occur when
the energy of a bound state E0
in a closed channel coincides
with the scattering energy E (see figure beside).
The coupling between the curve V1
and V2 (e.g., due to hyperfine
and Zeeman interactions) enhances the mixing of the corresponding
wave functions
ψ0
and ψreg.
In the case of a magnetically tuned Feshbach resonance, the scattering
length can then be parametrized as
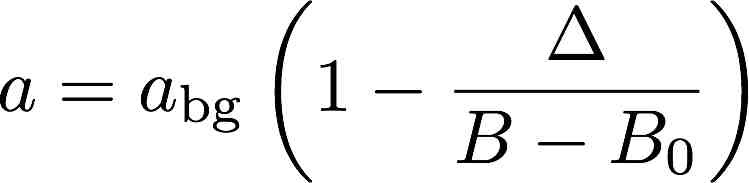 ,
,
where the background value
abg
varies slowly, while B
0 and Δ
are the position and width of the resonance.
In our group, we determine the value of the scattering length
for a variety of systems, including the effect of Feshbach
resonances. We include the effect of various interactions
(Zeeman, hyperfine, dipolar, etc.) to obtain the cross sections
and scattering length.
 Beside the very important application of ultracold
scattering to atomic samples, the same tools and concepts
can also apply to ultracold chemistry. The same expressions
for the cross sections can be found, although the calculations
are more involved. Our group has been exploring benchmark
systems in the ultracold regime, namely
H2 + D → HD + H, or
HCl+H → H2 + Cl.
We used these systems to study the effect of near threshold
resonance (NTR) on the cross sections.
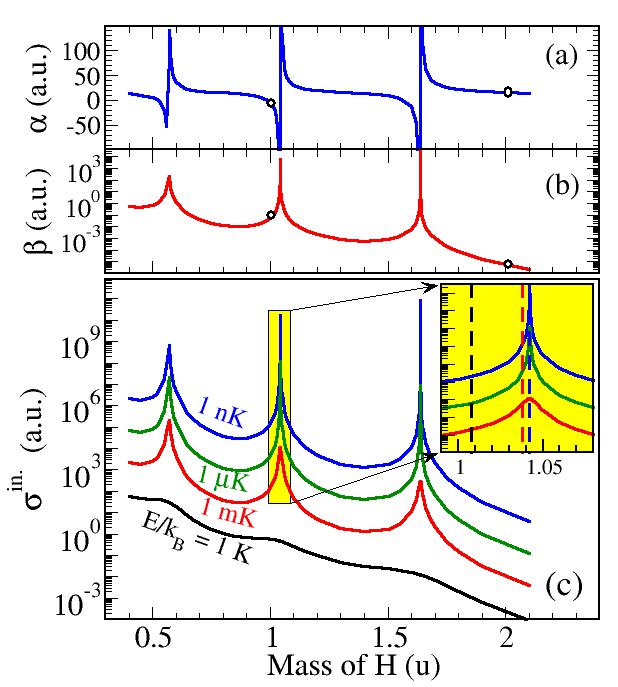
For example, by varying the mass of hydrogen in our calculations,
we scanned regions where such NTR occurs, as illustrated in the Figure
beside, where (a) shows α, (b) β, and (c) the inelastic
cross section for different scattering energies (in temperature units).
The resonances correspond to the sharp peaks (and the real mass of hydrogen
and deuterium are shown as open circles). We found that
the total inelastic cross section reaches a new "universal" regime
for momentum nearing a "resonant" value.
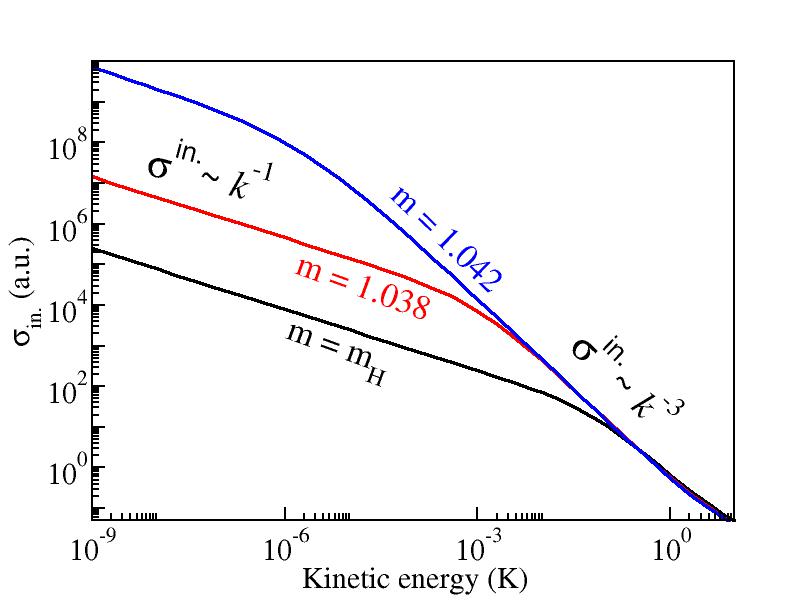
Taking three particular masses corresponding to the vertical dashed lines
in the inset of (c), we illustrate this effect in the following figure;
the cross section behaves as
k-3
instead of the usual Wigner's
k-1
regime.
We are exploring NTRs in the case of Feshbach resonances,
as well in Efimov states (related to three-body interactions).
Beside the very important application of ultracold
scattering to atomic samples, the same tools and concepts
can also apply to ultracold chemistry. The same expressions
for the cross sections can be found, although the calculations
are more involved. Our group has been exploring benchmark
systems in the ultracold regime, namely
H2 + D → HD + H, or
HCl+H → H2 + Cl.
We used these systems to study the effect of near threshold
resonance (NTR) on the cross sections.
For example, by varying the mass of hydrogen in our calculations,
we scanned regions where such NTR occurs, as illustrated in the Figure
beside, where (a) shows α, (b) β, and (c) the inelastic
cross section for different scattering energies (in temperature units).
The resonances correspond to the sharp peaks (and the real mass of hydrogen
and deuterium are shown as open circles). We found that
the total inelastic cross section reaches a new "universal" regime
for momentum nearing a "resonant" value.
Taking three particular masses corresponding to the vertical dashed lines
in the inset of (c), we illustrate this effect in the following figure;
the cross section behaves as
k-3
instead of the usual Wigner's
k-1
regime.
We are exploring NTRs in the case of Feshbach resonances,
as well in Efimov states (related to three-body interactions).
We also investigate the effect of Rydberg-dressing on the interaction in
the atom-diatom system, by using a laser far-detuned from a highly-excited
Rydberg state. Basically, by mixing a little bit of Rydberg character
into the wave function of the system, the polarizability and hence
the van der Waals complex is affected. We recently found that it is
possible to tune chemical
reaction rates using such Rydberg-dressed interaction. This approach
is in principle very general, since all atomic or molecular systems do possess
Rydberg states usable for modifying interactions. More details are given
in a recent PRL (see also
Rydberg Physics for more details)..