The large impact of information technology on our society
is fueled by the rapid increase in computing power, described
by Moore's law: processor power doubles every 18 months. This
is accompanied by a reduction in the size of the processors,
and when the actual processors based on classical treatment
of information will reach the quantum limit, the uncertainty
principle of quantum mechanics will come into play. Quantum
information science (QIS) is investigating the treatment of
information based on fundamental quantum principle, such as
interference and entanglement
 Advances in QIS indicate that quantum computing devices can
perform certain tasks considerably more efficiently than any
classical computers, by using quantum states superpositions
to create quantum bits, or qubits. Quantum cryptography protocols
have been successfully implemented, and quantum algorithms
offering potentially enormous speed-up are being developed,
e.g., for factoring (Shor) or database search (Grover)
algorithms. Adapting known classical algorithms to their
quantum counterparts, such as classical to quantum random
walks (QRW) is being pursued. Recently, QRW have been featured
in algorithms with provable exponential speedups.
Advances in QIS indicate that quantum computing devices can
perform certain tasks considerably more efficiently than any
classical computers, by using quantum states superpositions
to create quantum bits, or qubits. Quantum cryptography protocols
have been successfully implemented, and quantum algorithms
offering potentially enormous speed-up are being developed,
e.g., for factoring (Shor) or database search (Grover)
algorithms. Adapting known classical algorithms to their
quantum counterparts, such as classical to quantum random
walks (QRW) is being pursued. Recently, QRW have been featured
in algorithms with provable exponential speedups.
To exploit these possibilities, it is essential to address
coherently quantum states in a system and to perform reversible
quantum logic operations; preserving coherence is crucial since
quantum interference and entanglement are extremely fragile.
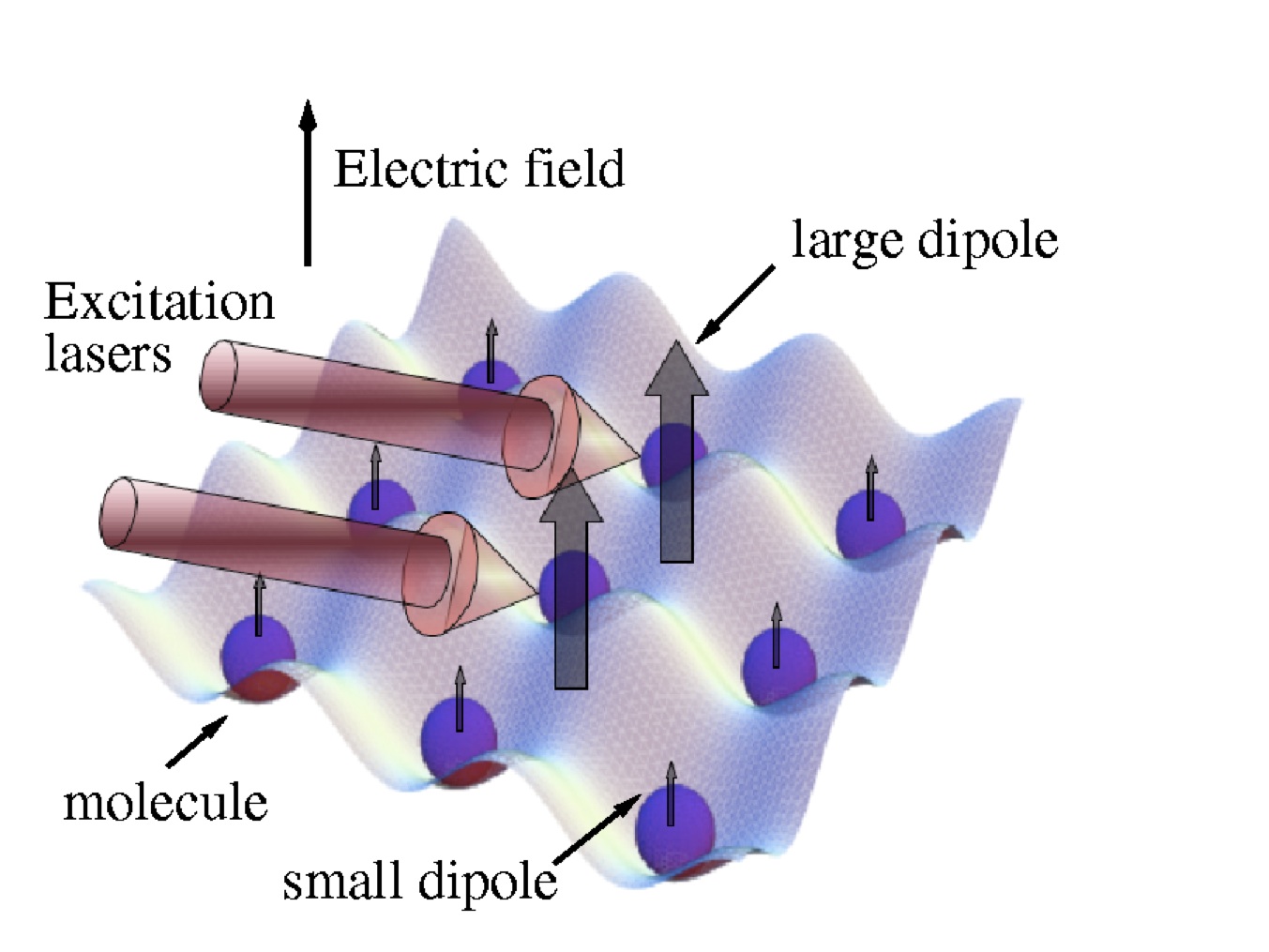
Many platforms are investigated in quantum information: cold
trapped ions, neutral atoms or polar molecules in optical lattices
(see figure beside), atoms in crystals, spin of particles,
photons in cavity QED or nonlinear optical setups,
or mesoscopic ensembles.
In our group, we study a variety of atomic and molecular platforms:
ultracold Rydberg atoms, polar molecules, hybrid atom-molecule or
atom-ion systems. All of them exhibit conditional interactions
that can be used to implement quantum gates. We use Rydberg atoms
to illustrate the basic ideas.
Rydberg atoms posses extreme properties which scale rapidly
with principal quantum number
n.
In particular, their dipole moment and polarizability scale as
n2
and n7,
respectively. Together with the small spacing between Rydberg levels
(scaling as
n-3),
these lead to large interactions between Rydberg atoms, scaling
as n4/R3 and
n11/R6 for dipole-dipole
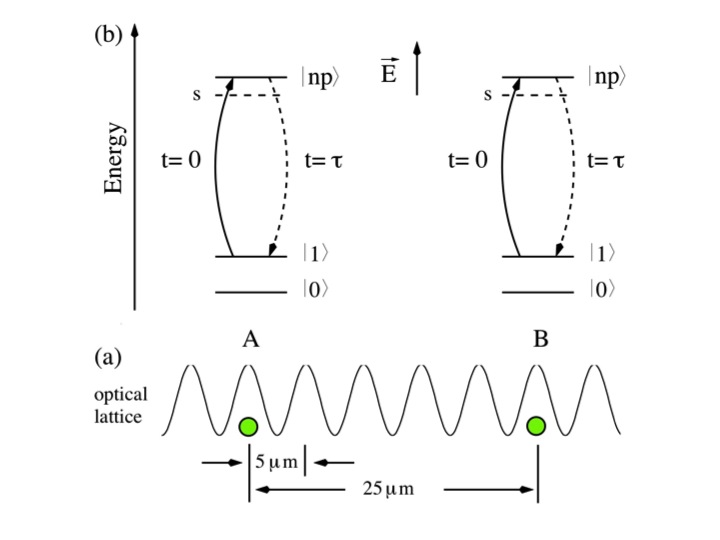
and van der Waals types, respectively. So, if we consider two atoms
separated by a distance R
(see Fig (a) below), each one
can be in its ground state |g⟩ or an excited Rydberg state |e⟩,
the pair of atoms interact strongly only if both are in |e⟩,
leading to a conditional interaction.
 We proposed to use such
conditional excitation to implement a phase gate using atoms
initially in a superposition of "ground" states (labeled |0⟩ and
|1⟩) and laser pulses to selectively excite a specific state
(say |1⟩) into the Rydberg state |e⟩. In alkali atoms,
such as 87Rb, one could use
two different hyperfine states
such as |f,m⟩=|1,-1⟩ and |2,2⟩ for |0⟩ and |1⟩,
respectively, and |np⟩ for the Rydberg state. Assuming that
atoms A and B are both prepared in a superposition state like
|0⟩ + |1⟩, the initial state of the 2-atom system is
We proposed to use such
conditional excitation to implement a phase gate using atoms
initially in a superposition of "ground" states (labeled |0⟩ and
|1⟩) and laser pulses to selectively excite a specific state
(say |1⟩) into the Rydberg state |e⟩. In alkali atoms,
such as 87Rb, one could use
two different hyperfine states
such as |f,m⟩=|1,-1⟩ and |2,2⟩ for |0⟩ and |1⟩,
respectively, and |np⟩ for the Rydberg state. Assuming that
atoms A and B are both prepared in a superposition state like
|0⟩ + |1⟩, the initial state of the 2-atom system is
|Q0 ⟩ ∝
|00⟩ +|01⟩ + |10⟩ + |11⟩
where |ij⟩ ≡ |i⟩A
⊗ |j⟩B stands
for the atom A in state i and atom B in state j, respectively.
At time t=0, the state |1⟩ of each atom is excited to the
Rydberg state |e⟩ (see Fig.(b)) leading to the initial state
|Qinit ⟩ ∝
|00⟩ +|0e⟩ + |e0⟩ + |ee⟩ .
Because only |ee⟩ experiences a strong interaction V (e.g.,
∝ n
4/
R3
for dipole-dipole or ∝
n11
/R
6 van der Waals interactions),
it will acquire a phase φ(t)=V t/ℏ, so that
|Q(t) ⟩ ∝
|00⟩ +|0e⟩ + |e0⟩ + eiφ
|ee⟩.
After a time t=τ such that φ=π, the Rydberg state |e⟩ of
each atom is stimulated back into |1⟩ (see Fig.(b)), leading to the final
state
|Qfinal ⟩ ∝
|00⟩ +|01⟩ + |10⟩ - |11⟩ .
 This final state is an example of an entangled state, i.e. a state that
cannot be written as a product state of atom A and atom B: the states of
both atoms are intertwined. The sequence of pulses described
above leads to a universal two-qubit quantum gate, namely the
phase gate, where the sign of |mn⟩ is changed only if both
m=n=1. It can be summarized as
This final state is an example of an entangled state, i.e. a state that
cannot be written as a product state of atom A and atom B: the states of
both atoms are intertwined. The sequence of pulses described
above leads to a universal two-qubit quantum gate, namely the
phase gate, where the sign of |mn⟩ is changed only if both
m=n=1. It can be summarized as
|mn⟩ → eimnπ
|mn⟩ with m, n = 0, 1.
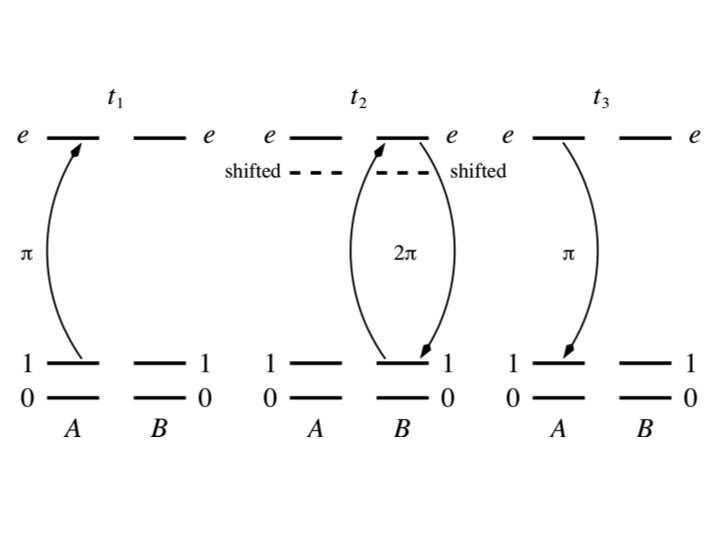
We also put forward another pulse sequence leading to a phase gate
based on the blockade mechanism, originally proposed for Rydberg
atoms. It assumes that atoms are far enough from each other to
be separately addressed by lasers, while retaining a strong enough
interaction between Rydberg atoms to maintain the excitation
blockade. As a result, because the doubly-excited state |ee⟩
is shifted out of resonance (see Fig. beside), it cannot be
populated, again leading to a conditional excitation. By shining
a π-pulse laser on site A at time t1,
followed by a 2π-pulse on site B at t2
(which populates the state |e⟩B
and brings it back to |1⟩B only
if |e⟩A is not populated —
otherwise nothing happens because of the excitation blockade), and
finally applying a final π-pulse on site A at
t3, we obtain the following
| field/pulse |
|
initial state |
|
|
|
final state |
|
comment |
|
|
EA / π
|
|1⟩A
|1⟩B
|
→
|
i |e⟩A
|1⟩B
|
A makes a transition
|
|
|
|1⟩A
|0⟩B
|
→
|
i |e⟩A
|0⟩B
|
A makes a transition
|
|
EB / 2π
|
|e⟩A
|1⟩B
|
→
|
|e⟩A
|1⟩B
|
blockaded: no transition
|
|
|
|0⟩A
|1⟩B
|
→
|
i2
|0⟩A
|1⟩B
|
B makes a transition up and down: π-phase shift
|
|
EA / π
|
i |e⟩A
|1⟩B
|
→
|
i2
|1⟩A
|1⟩B
|
A makes a transition
|
|
|
i |e⟩A
|0⟩B
|
→
|
i2
|1⟩A
|0⟩B
|
A makes a transition
|
After the pulse sequence, only
|0⟩A|0⟩B has not been modified:
all others are multiplied by -1. The resulting state is again
an entangled state, and this sequence also gives a phase gate:
|mn⟩ → ei(δmn-mn)π
|mn⟩ with m, n = 0, 1.
In addition to exploring similar concepts in other AMO platforms
(e.g., polar molecules, hybrid atom-molecule or atom-ion systems),
our group also investigate how the strong interactions between
Rydberg atoms could be used to study and implement Quantum Random
Walk (QRW).
 Advances in QIS indicate that quantum computing devices can
perform certain tasks considerably more efficiently than any
classical computers, by using quantum states superpositions
to create quantum bits, or qubits. Quantum cryptography protocols
have been successfully implemented, and quantum algorithms
offering potentially enormous speed-up are being developed,
e.g., for factoring (Shor) or database search (Grover)
algorithms. Adapting known classical algorithms to their
quantum counterparts, such as classical to quantum random
walks (QRW) is being pursued. Recently, QRW have been featured
in algorithms with provable exponential speedups.
Advances in QIS indicate that quantum computing devices can
perform certain tasks considerably more efficiently than any
classical computers, by using quantum states superpositions
to create quantum bits, or qubits. Quantum cryptography protocols
have been successfully implemented, and quantum algorithms
offering potentially enormous speed-up are being developed,
e.g., for factoring (Shor) or database search (Grover)
algorithms. Adapting known classical algorithms to their
quantum counterparts, such as classical to quantum random
walks (QRW) is being pursued. Recently, QRW have been featured
in algorithms with provable exponential speedups.
 We proposed to use such
conditional excitation to implement a phase gate using atoms
initially in a superposition of "ground" states (labeled |0⟩ and
|1⟩) and laser pulses to selectively excite a specific state
(say |1⟩) into the Rydberg state |e⟩. In alkali atoms,
such as 87Rb, one could use
two different hyperfine states
such as |f,m⟩=|1,-1⟩ and |2,2⟩ for |0⟩ and |1⟩,
respectively, and |np⟩ for the Rydberg state. Assuming that
atoms A and B are both prepared in a superposition state like
|0⟩ + |1⟩, the initial state of the 2-atom system is
We proposed to use such
conditional excitation to implement a phase gate using atoms
initially in a superposition of "ground" states (labeled |0⟩ and
|1⟩) and laser pulses to selectively excite a specific state
(say |1⟩) into the Rydberg state |e⟩. In alkali atoms,
such as 87Rb, one could use
two different hyperfine states
such as |f,m⟩=|1,-1⟩ and |2,2⟩ for |0⟩ and |1⟩,
respectively, and |np⟩ for the Rydberg state. Assuming that
atoms A and B are both prepared in a superposition state like
|0⟩ + |1⟩, the initial state of the 2-atom system is
 This final state is an example of an entangled state, i.e. a state that
cannot be written as a product state of atom A and atom B: the states of
both atoms are intertwined. The sequence of pulses described
above leads to a universal two-qubit quantum gate, namely the
phase gate, where the sign of |mn⟩ is changed only if both
m=n=1. It can be summarized as
This final state is an example of an entangled state, i.e. a state that
cannot be written as a product state of atom A and atom B: the states of
both atoms are intertwined. The sequence of pulses described
above leads to a universal two-qubit quantum gate, namely the
phase gate, where the sign of |mn⟩ is changed only if both
m=n=1. It can be summarized as