Section 6.1
Assume the following diagram gives you the frequencies of the resonant modes of a rectangular cavity as you change the length of one of the sides:
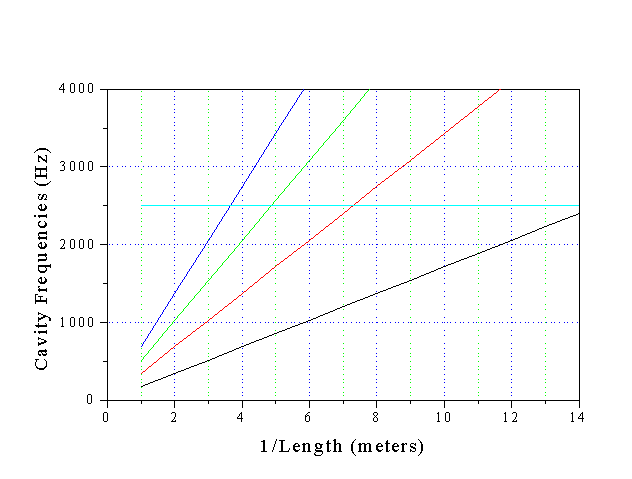
a) Label the line with "g1" which represents the fundamental mode in the direction that does NOT change.
b) Label the line "f2" which represents the second mode in the direction that does change.
c) Sketch the line which would represent the combination frequency,
d) At what length does f2 = g1?
Once again we have a rectangular cavity in which one side is kept fixed while the other side is varied. We plot the resonant frequencies as a function of 1/L were L is the length that we are changing:

If f1, f2, f3 Â represent the series of regular resonances in the direction we are changing and g1, g2, g3 .. represent the series of regular resonances in the fixed direction, answer the following:
a) Over what range of lengths would the order of resonances going from low frequency to high frequency be:
b) Over what range of lengths would the order of resonances going from low frequency to high frequency be:
c) What is the ordering of the first four frequencies at a length of 0.05 meters?
d) At what length does
Using the graph above, answer the following questions:
a) Label f1, f2, g1, g2.
b) Over what range of lengths would the order of resonances going from low frequency to high frequency be:
c) What is the ordering of the first four frequencies at a length of 0.2 meters?
d) At what length does
Assume that we have an closed-open air column with a length of 30 cm. We connect a speaker and microphone together through an amplifier with the following overall gain profile:
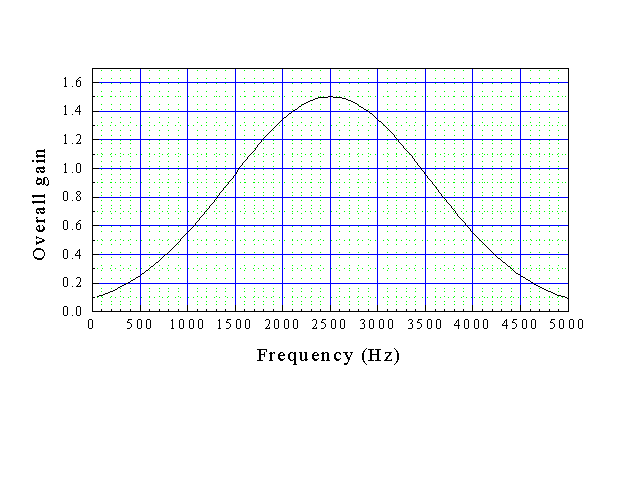
a) What are the frequencies of the modes which could exhibit feedback?
b) Which mode will dominate?
a) If we connect a speaker and microphone together through an amplifier with the following overall gain profile, over what frequency range can we get feedback?
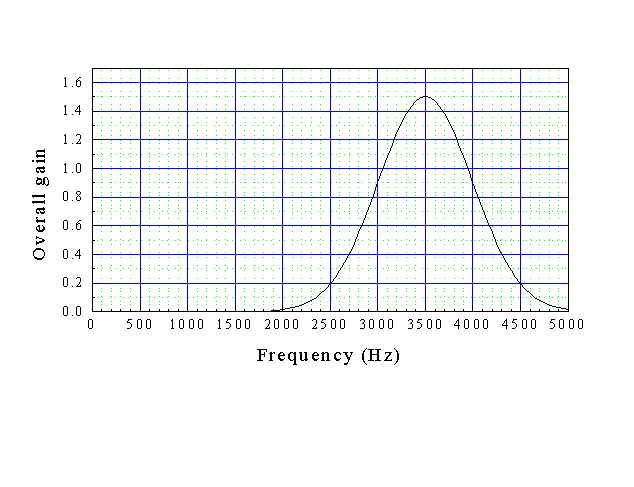
b) Now, consider that we have a closed-closed air column. If we only want one mode to exhibit feedback we want the frequency interval between modes to equal the frequency range from part a). What is the maximum length air column that will only have one mode in this range?
An amplifier can provide gain only up to a certain frequency:

a) Below what frequency can feedback occur?
b) If you use a closed-closed air column as a resonator, what is the longest length you can use and only have one mode experience feedback?
The following is a plot of the gain of an amplifier as a function of frequency:
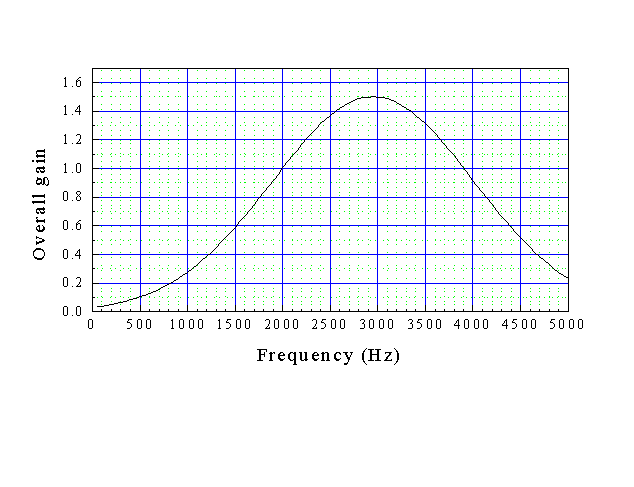
a) Over what frequency range can feedback occur?
b) If this were the gain in a closed-closed air column, over what range of lengths of the air column would both the second harmonic, 2f and the third harmonic 3f both experience feedback?

a) You have a closed-closed air column with a length of 34.3 cm. The graph above gives the overall gain in a feedback loop. At what frequencies will you have feedback? (There are 2).
b) Where along the tube would you place the microphone to make sure that you get feedback on the lower of the two frequencies?
c) Where along the tube would you place the microphone to make sure that you get feedback on the higher of the two frequencies?
An amplifier can provide gain only up to a certain frequency:

a) Below what frequency can feedback occur?
b) If you use a closed-closed air column with a length of 17 cm as a resonator, will the fundamental mode show feedback?
c) If yes, should you lengthen or shorten the tube to prevent feedback?
If no, should you lengthen or shorten the tube to get feedback?
a) Sketch individual modes and the nodal lines for an air cavity, closed all sides, in the mode consisting of the fourth mode in the horizontal direction and the second mode in the vertical direction.
b) If the horizontal dimension is 1.10 meters and the vertical dimension is .37 meters, what is the frequency of the mode described in part a)?
c) If I created a feedback loop with this cavity, mark a position on the rectangle above where I could place a microphone to ensure that I get feedback on the horizontal mode but not the vertical?
This rectangular cavity has dimensions of 17.15 cm by 10 cm.
a) First assume the microphone is placed at the position marked (1). Find the frequencies of the first three modes that can show feedback. You will need to think about where the nodal lines for each mode are.
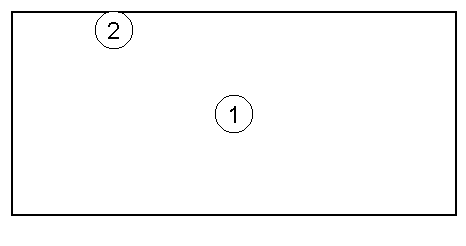
b) Now assume the microphone is placed at the position marked (2). Again, find the frequencies of the first three modes that can show feedback.
Section 6.2
Section 6.3
a) A siren on a fire truck operates at 1000 Hz. While the truck is coming at you 66.3 miles/hour, what frequency do you hear?
b) After it goes by, what frequency do you hear?
c) By how many half steps does the frequency change?
a) An ambulance is traveling at 70 miles/hour and sounds a siren at 2000 Hz. If you are standing by the side of the road and the ambulance is traveling away from you, what frequency do you hear?
b) If you are now following the ambulance also at 70 miles/hour it is not clear what frequency you will hear. However, you can consider that you are a moving observer hearing the Doppler shifted frequency from part a). What frequency do you hear?
Two fire alarms go off and you find yourself caught in between them. The frequency of the alarms is 850 Hz.
a) If you start running towards one to get out of the building at 5.5 m/sec, what frequency do you hear from each speaker?
b) What is the frequency and period of the beat between the two alarms?
c) When you are right in the middle of the two alarms, there will be constructive interference, so the alarms will sound loud. How far do you have to move to be at the next point where you have constructive interference?
d) How long will it take you to move this distance at a speed of 5.5 m/sec?
e) How does this time compare to the period of the beat frequency in b)?
a) A stationary siren produces two frequencies, 1050 Hz and 1150 Hz. If you are moving away from the siren at 25 m/sec, what beat frequency do you hear?
b) In part a), does the beat frequency change depending on whether or not you are moving?
c) How do these results affect the transmission of music over radio waves? In other words, are the frequencies that you hear while listening to the radio affected by the Doppler shift? Remember that acoustic frequencies are sent as beat frequencies of the radio waves.
One train is stopped in a station while another train is entering the station at 35 miles/hour. Both trains are blowing their horns at 1500 Hz. The air is still.
a) If you are sitting in the stopped train what beat frequency would you hear between the two horns?
b) If you are sitting in the moving train, what beat frequency would you hear?
c) Now the first train leaves the station at 35 miles/hour traveling in the opposite direction to the incoming train. What beat frequency would you hear if you were standing on the platform?
a) Assume you are in a physics lab with a speaker at each end emitting an annoying frequency of 3000 Hz. As you try to escape the lab at 3 meters/sec one frequency will be shifted up and the other down. By how much will they be shifted?
b) What will be the beat frequency between the two frequencies that you hear?
c) These speakers form a standing wave. What is the separation between the nodes?
d) If you are moving at 3 meters/sec, how many nodes will you pass per second?
e) How does this relate to part b)?
a) You are in a truck traveling at 40 miles/hour and an ambulance with a siren at 2000 Hz going 70 miles/hr passes by you. The air is still. We want to figure what frequency you will hear. Two steps are required to solve this problem. Fill in the following table to set-up the problem.
b) Now that you have set the problem up, calculate the final frequency that you will hear.
|
Moving source or observer? |
What speed? |
Frequency goes up or down? |
Step 1 |
|
|
|
Step 2 |
|
|
|
Many times, the Doppler shift is used under conditions where a wave is reflected off of a target (like a police radar detector used to catch speeders or bats looking for an insect). However, calculating the Doppler shift becomes a little more complicated.
a) A bat is flying towards a wall at 10 m/sec and emits a pitch of 10,000 Hz. What frequency would a bug on the hear (if it could hear)? Here, the bat is a moving source and the wall is stationary.
b) The reflected sound will have the same frequency as that heard by the bug, in other words, the Doppler shifted frequency. What frequency would the reflected wave appear to have for the bat? Now, the bat is a moving observer.
c) The bat actually listens for the beat frequency between the sound it emits and the reflected sound. What would be the beat frequency in this case?
Many streetlights contain sodium atoms, which strongly give off yellow light at two wavelengths: 589.00 nm and 589.59 nm. 1 nm = 10-9 m.
a) What frequencies do these wavelengths correspond to and what is the beat frequency between them?
b) If a spaceship is approaching the Earth at 5x106 m/sec, what frequencies would the pilot measure from the streetlights, and what would be the new beat frequency
The Doppler shift of light is an extremely important tool for astronomers, as they can use it to measure how fast distance objects are moving. Atoms, like hydrogen, emit light at specific wavelengths. Since the Doppler effect changes the frequency of the wave it also changes the wavelength.
a) Hydrogen emits a particularly strong line at 121.5 nm. What frequency does this correspond to?
b) If a star is moving away from us at 3x106 m/sec, what frequency would we measure?
c) What is the change in wavelength
In order to get a large Doppler shift, the source or observe must be traveling at a reasonable fraction of the velocity of the wave. However, police officers can use the Doppler shift of microwaves to accurately measure the velocity of a car, which is MUCH less than the speed of light. The precision comes from measuring beats. Police radar uses a frequency of 109 Hz.
a) If the police officer is standing by the side of the road, what is the frequency of the radar that you would detect in your car after you pass by at 60 miles/hr = 27 m/sec)?
b) The microwaves reflected by the car now act as a moving source as they travel back to the police officer. What is the frequency of the reflected microwaves that the police officer would detect?
c) What is the beat frequency between the original radiation and the reflected radiation? This beat frequency can be very accurately measured.
a) A trumpet player standing on the side of a lake sounds an A with a frequency of 440 Hz. You are in a motor moving away from the shore at a speed of 13 m/sec. With respect to the medium, which is moving, the source or the observer and what frequency do you hear? The air is calm.
b) Now the wind is blowing in the same direction and with the same speed as the motorboat. Again, with respect to the medium, which is moving, the source or the observer and what frequency do you hear?
c) At this point the wind reverses direction, but still has a speed of 13 m/sec. Now what frequency do you hear?
a) A trumpet player standing on the side of a lake sounds a middle C with a frequency of 256 Hz. You are in a motor boat moving away from the shore at a speed of 8 m/sec. What frequency do you hear? The air is calm. Which is moving, the source or the observer?
b) Now the wind is blowing in the same direction and with the same speed as the motor boat. What frequency do you hear? Which is moving, the source or the observer?
c) At this point the wind reverses direction. Now what frequency do you hear?
An orchestra is playing outside and the wind is blowing. We want to see how this effects the tuning of the instruments. If the oboe player plays an "A" at 440 Hz and the wind is blowing at 20 miles/hour what frequency will be heard by the players upwind from the oboe? What frequency will be heard downwind?

You are sailing between to banks of a lake. The wind is blowing at 12 m/sec from left to right and the boat is moving in the same direction at exactly the same speed. A siren is sounding on each bank at the same frequency of 1750 Hz.
a) On the boat, what frequencies do you hear from the left and right siren?
b) What is the beat frequency between these two Doppler shifted frequencies?
a) A space ship is approaching the earth at 90% of the speed of light, announcing its arrive at a radio frequency of 91.7 MHz. Using the normal formula for Doppler shifts, what frequency would we receive the message at?
b) Now use the relativistic formula. What frequency would we receive?
c) These frequencies are quite different and can be used to confirm EinsteinÂs theory of relativity.
Section 6.4
a) Under what conditions can something produce a sonic boom? How fast must it be traveling?
b) How can you use the effect of a sonic boom to illustrate the difference between a moving source and a moving observer? Use the equations for each to support your answer.
a) If you are sitting at the edge of a pond and you dip your toe into the water you will create water waves. If a bug is sitting on a leaf in the middle of the pond it will eventually feel the water waves. Who is the source, who is the observer and is either one moving?
b) Now you are sitting at the edge of a stream. Again, you dip your toe into the water to create waves and they are felt by a bug moving along with the water. With respect to the water, who is moving and who is stationary?
c) If the water is flowing down the river faster than the speed of the water waves, can you make any waves travel upstream? What is this situation similar to?
a) The pilot of a jet airplane is trying to break the sound barrier. His speedometer always gives his speed with respect to the ground. If there is no wind blowing, how fast must he travel to break the sound barrier?
b) Now, assume that the wind is blowing at 200 miles/hour. If the plane is flying into the wind, how fast, with respect to the ground, must he fly to break the sound barrier? If he is flying with the wind, how fast must he go?
c) You are in a hurricane and you hear a cow mooing, which is being carried along with the wind. Who is the source, who is the observer and which is moving?
d) The storm gets really bad and the winds reach 800 miles/hour. If you stay fixed to the ground, would you produce a sonic boom? Why or why not?
Assume you are in the desert trying to break the sound barrier in a race car. There are two people, one standing at the start line and one at the finish. You have a siren at a frequency of 2500 Hz.
a) When you reach a speed equal to one half of the speed of sound, what frequency will the person at the start line hear from the siren?
b) When you reach a speed equal to one half of the speed of sound, what frequency will the person at the finish line hear from the siren?
c) If the wind is blowing at 40 miles/hr from the start line towards the finish line, how fast would you have to drive with respect to the ground to break the sound barrier?
d) If the wind is blowing at 40 miles/hr from the finish line towards the start line, how fast would you have to drive with respect to the ground to break the sound barrier?
A fighter jet is going at Mach 3, which is 3 times the speed of sound. What is the opening angle of the cone produced by the sonic boom?
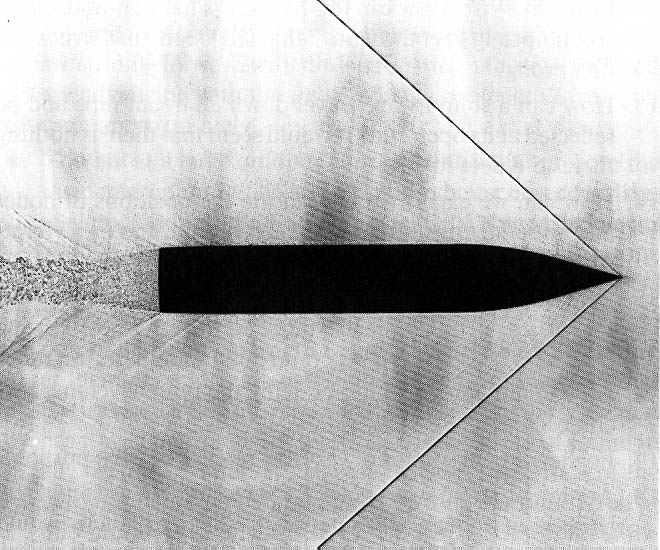
The bullet in this picture is moving in air. How fast is it moving?
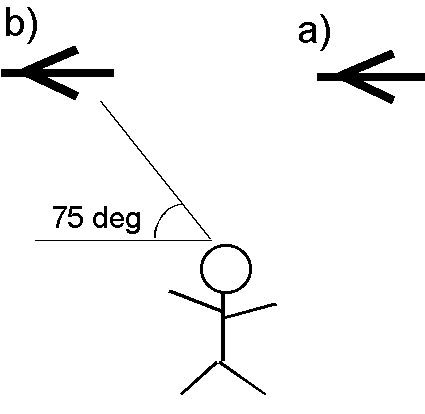
You are looking up in the sky when you notice an airplane (flying from right to left in the figure). Assume that the speed of sound is 767 miles/hour.
a) When the airplane is at position a) what can you tell about the airplanes speed if you can hear it, or if you cannot hear it?
b) If you cannot hear the airplane until after it flies directly overhead to a position that is at 75° with respect to the horizontal (position b)), how fast is the airplane flying?
a) If you are sitting at the edge of a pond and you dip your toe into the water you will create water waves. If a bug is sitting on a leaf in the middle of the pond it will eventually feel the water waves. Who is the source, who is the observer and is either one moving?
b) Now you are sitting at the edge of a river. Again, you dip your toe into the water to create waves and they are felt by a bug moving along with the water. With respect to the water, who is moving and who is stationary?
c) The water is flowing down the river at 0.75 meters/sec and the speed of the water waves is 0.3 meters/sec. A log sticks straight out of the water and ripples form around the log. What angle, q, will the ripples make?
