Throughout this course we have mainly focused on sound waves, as that is the most important wave for music. We also have considered waves on strings and on metal bars, as each of these gives rise to a whole class of musical instruments. However, there is another type of wave that is extremely important to physics and science and our everyday life, and that is light waves. Given what we already know about waves, in general, adding light to our list of waves will not be so difficult, although light does have some rather unusual properties. As discussed in Section 5.1, all waves share a variety of properties, and we will examine light waves along these same lines.

The medium for most waves is usually apparent. For a string wave, the medium is a string. For sound waves, the medium is air. What is the medium for light? We know that we can detect the light from distant stars and galaxies, so apparently light can travel through empty space. So, does this mean that light does not require a medium, or does it mean that empty space is not so empty, after all? As soon as it was realized that light is a wave, the question of its medium has plagued physicists up to this day. At this point, the answer seems rather clear, as light is now quite well understood, but the conclusion is startling: light, indeed, does require a medium and, thus, space is not empty! Space is filled by a "sea" of positrons and electrons that, normally, we are not aware of. However, under certain extreme conditions, these positrons and electrons can be detected. The properties of this unusual medium is still an active area of research, today.

Even if the medium is still not well understood, the restoring force is. The restoring force for light is comprised of the more familiar electric and magnetic forces. Electric forces drive electricity through wires and the magnetic force is what makes magnets attract or repel each other.

As we have discussed before, waves really have an existence of their own because they can carry energy. Moreover, waves are different from normal objects because they are always in motion – they are always moving with the speed characteristic of that particular wave. Both of these features make light waves very useful in a wide range of situations.

At the most basic level, nearly all of the energy that keeps the Earth warm and keeps us alive on the Earth comes, indirectly or indirectly from the Sun, in the form of light. Indeed, the amount of energy striking the Earth in the form of light is staggering: 5*10¹⁷ joules of energy per second. Even if only a tiny fraction of this can be harnessed, our energy problems would be solved.

The light also delivers energy very quickly: the speed of light is 3*10⁸ m/sec, or, perhaps the more familiar 186,000 miles/sec. Another odd property of light is that this speed sets the absolute speed limit for everything in this Universe – nothing can travel faster than light. This speed is unimaginably fast, but it is not instantaneous. In fact, the Sun is so far away, that is still takes 8 minutes for the light of the Sun to reach the Earth. Because of the relationship fl = v, the very large speed of light affects the range of wavelengths and frequencies that we encounter with light.

Light waves that we come across in daily life cover a huge range of frequencies:

Starting at the "low" frequency end of the spectrum of light, we find radio waves. When you set your AM radio to 1040, you are really selecting the frequency of radio waves that you want to receive. Each radio station is given its own frequency to keep its transmissions separate from everyone else’s. The 1040 corresponds to 1040 kHz, or about 1 MHz. This is right in the range of radio frequencies in the diagram above. If you listen to 104 on the FM dial, this corresponds to 104 MHz.

Although these frequencies are very large compared to the frequencies we are used to from sound waves, they do represent the low end of the spectrum. As we get up to frequencies of around 1 GHz (10⁹ Hz) we find the waves responsible for TV transmission and cell phone communications.

Even higher frequencies lead to microwaves, as in the waves used in microwave ovens. Here, it is quite clear that light waves are being used for their ability to carry energy!

All the uses of light waves is too vast a topic to cover here, but looking at the diagram again, we also see infrared, visible, ultraviolet, and x-ray waves. Although the uses and applications of these waves are incredibly diverse, they are all as similar to each other as the different notes on the piano are! All of these waves are simply light waves of different frequencies.

Waves are classified into two groups: transverse or longitudinal. This indicates how the direction of motion of the medium is related to the direction of motion of the wave, itself. Remember, for a string wave, the string moves perpendicular to the string, while the wave travels along the string. Thus, a string wave is a transverse wave. For sound waves, the air molecules move along the motion of the wave, and hence, sound is a longitudinal wave.

What is light: longitudinal or transverse? This is obviously a hard question to answer, since we hardly understand the medium that it is moving in! However, we can deduce what it must be. For a longitudinal wave, there is only one direction for the medium to move along – the direction that the wave is moving. However, for transverse waves, there are always two directions that are perpendicular to the direction of the wave. For a string wave this may be up and down and back and forth, if the wave is traveling left to right. So, if we can determine whether there is only one direction for the medium to vibrate, or two, we can determine if the wave is longitudinal or transverse.

As it turns out, there are two directions for light waves to oscillate and, consequently light is a transverse wave. Although this may all seem rather obscure, the item needed to prove this is quite ordinary – a pair of polarized sunglasses will work! When you put on a pair of sunglasses the amount of light reaching your eyes is cut approximately in half. This makes things more comfortable for your eyes, but how is the light level reduced? It may be that the lenses simply absorb half the light, and, in fact, regular non-polarized sunglasses do just that. If you place a second pair of regular sunglasses right in front of the first, the light level will again be cut in half, and now only a quarter of the light will reach your eyes.

However, if you perform the same experiment with the polarized sunglasses, something completely different happens. If you look through one pair of polarized glasses, the light is cut in half, as we have said. But, now, if you look through a second pair, no additional light is lost! One pair of polarized glasses cuts just as much light as two. Now for the strangest part: if you rotate the second pair of polarized glasses by 90 degrees with respect to the first pair, you see nothing! All of the light is gone. As bizarre as this seems, it has a perfectly reasonable explanation related to the fact that light is a transverse wave.

As we discussed, transverse waves have two directions that they can vibrate in that are perpendicular to the direction that the wave is traveling. These two directions are called polarizations (which is where the term for polarized sunglasses comes from). If you are looking out at a distance object, the light waves that you see are traveling straight at you. The two polarizations, or directions that the light vibrates in, are then up and down and left and right. Natural light contains roughly equal amounts of each polarization. What polarized glasses are able to do is block one polarization but not the other. For example, polarized sunglasses are set to absorb the left-right polarization. So, half the light is blocked and the scene is less bright. However, if you look through a second pair of polarized glasses, as well, the left-right polarization has already been removed, so there is no further change to the light. If, on the other hand, you rotate the second pair of glasses by 90 degrees, then the second pair will remove the up-down polarization. In this case, both the left-right and up-down polarizations are gone, and there is no light left!

Looking at materials through a polarizer, like sunglasses, can reveal important properties of materials that you cannot see with normal light. The first of the next two pictures shows a plastic CD case with normal light, while the second shows the same case under polarized light. Notice that the second one looks quite different. In fact, the patterns of light show where there is stress in the plastic – one of the things that polarized light can reveal.

One of the simplest ways to show that something is a wave is to show that it produces interference. Recall that in Section 5.4 we discussed that fact that electrons must be waves because they show constructive and destructive interference. In the same way, light must also be a wave because it shows interference.

There are many ways to show the interference of light and many applications based on interference, so we can only list a few, here. Perhaps the simplest demonstration of interference is to use a "double slit". The double slit is produced by creating two very fine slits in an opaque mask:

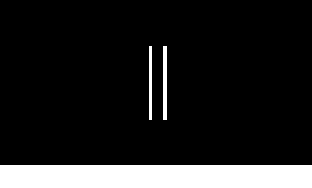
If you shine a bright light like a laser beam on this pair of slits, you produce to sources of light, very much like the two speakers in Section 5.4. From the top, it would look something like this:

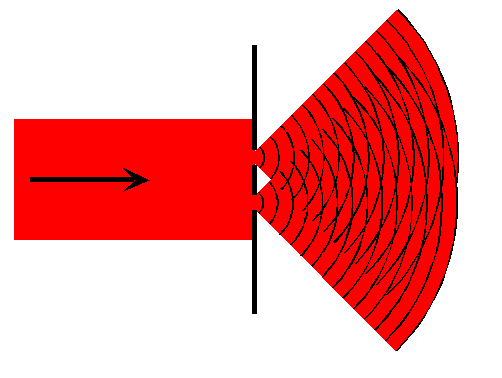
The two waves will interfere, just like the sound waves. In fact, the spacing of the points of constructive or destructive interference will follow exactly the same formula as in Section 5.4. Of course, you must use the correct wavelength for light waves.

In fact, all of the interference phenomena that we have discussed have a manifestation with light waves. Interference in reflection was already discussed. This leads to antireflection coatings for lenses. Also, bright colorful wrapping paper can be made, based on interference. A more precise and controlled application of this is holography. Here, the interference can create the impression of seeing something reproduced in 3-D.

Finally, interference of light waves in time has a very important application and that is radio transmission. Say you want to broadcast a note at 440 Hz. If you just play this note into a speaker sitting on top of a building, you would have to play it very loudly for others to hear it. Instead, you decide to use radio waves to transmit this sound. First, you must choose a radio frequency, like 91.7 MHz. This identifies you as the source of the sound, and anyone who wants to listen to you tunes into this frequency, but, so far, they will not hear anything. Now, to broadcast a note at 440 Hz, you actually transmit a second wave at 91.7 MHz + 440 Hz, or 91,700,440 Hz. Now, when someone tunes into 91.7 MHz, they will detect a beat frequency of 440 Hz. Both waves can be sent directly to a speaker. The speaker does not respond to the MHz frequencies, but it does respond to the acoustic beat frequency at 440 Hz.