In the last three sections, we have been considering various possibilities for the interference of two waves with the same frequency. This interference gives rise to a number of important and interesting effects. In this section, we explore a different situation: what happens when two waves with different frequencies interfere?

Although it may seem that this will make the problem more complicated, it actually leads to a rather simple result. To be begin the discussion, let’s consider two waves with different frequencies traveling in the same direction:

The top wave has a frequency of 10 Hz, while the bottom wave has a frequency of 11 Hz. One second of each wave is plotted, so the top wave shows 10 oscillations and the bottom wave, 11.

At the start, the two waves are in phase, that is, the peaks and valleys line up. At this point they add together constructively. In Section 5.2, we saw that two waves with the same frequency traveling in the same direction are always in phase or always out of phase. However, if we look at the figure above, this is not so for waves of different frequencies: after about five oscillations, we see that the waves are definitely out-of-phase: when one is a maximum the other is a minimum. So, at this point, there will be destructive interference. But this condition will not last, either. As the waves keep going, they come back into constructive interference. Of course, we can always just add the two waves together to see what it will look like:

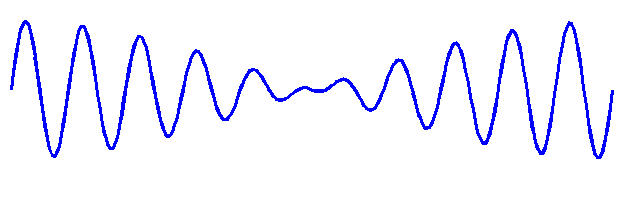
If we listened to this wave, we would first hear the sound normally as it started with constructive interference. The sound would then fade away as it went through destructive interference, and then come back again. This fading in and out will occur repetitively and so will have a period of its own, separate from the two waves. In the example above, we can see that the period for the wave to go from loud to soft and back to loud is 1 second. So, the sound will seem to pulse with a frequency of 1 Hz. The effect is known as beats. In this example, the beat frequency is 1 Hz, which happens to be the difference in frequency between the two original waves. This is true in general: two waves with frequencies f₁ and f₂, when added together, will pulse or beat with a frequency equal to the difference between the two original frequencies, f₁ and f₂. Since this frequency should always be a positive number, we can write:

f_beat = |f₁ – f₂|, where the symbol | | means the absolute value.

For example, if we play two notes, one at 500 Hz and one at 502 Hz, they will beat together with a frequency of 2 Hz. Or, if we play a note at 500 Hz and another at 625 Hz there will be a beat frequency of 125 Hz.

In terms of the basic physics, this is really all there is to the phenomenon of beats. It simply means that when more than one frequency is present, one must consider, in addition to the main frequencies, the beat frequencies between all of the main frequencies.

While the physics of beats is actually rather simple, how we respond to beats is probably the single most important consideration in all of music and how we perceive it! We will begin to unravel this rather strong statement here and return to it in much greater detail in Chapter 7.

It is not hard to see that beats are a complex phenomenon when it comes to perception. In the example just above, one note at 500 Hz and one at 502 Hz will beat at 2 Hz. Again, this means the sound will get louder and softer with a frequency of 2 Hz. Now, 2 Hz, or 2 oscillations per second is a frequency you can keep up with. If a clock is ticking at 2 Hz, you can count the individual ticks.

In contrast to this, the notes at 500 Hz and 625 Hz while beat at 125 Hz. Again, the sound will get louder and softer with a frequency of 125 Hz. But, how will the brain perceive this? Actually, this frequency is far too fast for the brain to follow individual oscillations, and so the brain does not interpret these beats as a periodic change in the loudness of the sound. In fact, under the right conditions, the brain interprets the beat frequency as its own frequency. In other words, you hear a new tone at 125 Hz! This is called a difference tone. We will return to this in Chapter 7.

Between these two extremes, there is a range of responses to beat frequencies:

1. Beat frequency is less than about 10 Hz.
   If the beat frequency is less than about 10 Hz, the two waves are very close in frequency and you will hear only one pitch (which is actually the average of the two frequencies). However, the loudness will vary with a frequency corresponding to the beat frequency.
2. Beat frequency roughly in the range of 10-60 Hz.
   This range of frequencies is quite significant and problematic for the human nervous system. It is too fast for the individual events to be discerned, but too slow for the brain to ignore. Phenomena in this frequency range can be quite annoying. For example, if a film is played at 10 frames/sec, you can identify the individual frames and it looks like a very fast slide show. If the film has more than 50 frames/sec, you don’t see the individual frames and the motion looks continuous. However, films at 20 – 30 frames/sec look very jerky and annoying. The brain does not know whether to focus on individual frames, or try to interpret it as continuous motion. Similar strobe lights at 20-30 Hz can easily produce headaches. When it comes to sound, beats frequencies in this range sound rough and dissonant – they are simply unpleasant to listen to. The pitches are too far apart to consider as one pitch, but too close together to distinguish. The brain cannot follow the individual beats but it is not fast enough to interpret as a new pitch. Simply put, when beats are present in this frequency range, the brain registers dissonance.
3. When the beat frequency is greater than about 60 Hz, the brain can distinguish the pitches of the two notes and the beat frequency is interpreted as a difference frequency, if at all.

These ranges depend somewhat on the absolute frequency of the two original notes, but, again, we will leave the details of this for Chapter 7.

As noted above, this range of frequencies is quite interesting for human perception and motor skills. If you hear taps in the range of 0-10 Hz, you can hear the individual taps. If the taps are greater than 60 Hz, they produce a pitch. However, in the range of 10-60 Hz, it is hard to interpret. However, it is also very hard to tap faster than about 10 Hz. The same is true of trills and vibrato – the periodic wavering of the pitch that can add warmth and richness to a note. So, motor skills are limited to this same frequency limit of about 10 Hz, but it is also right where interesting music effects are the most effective, such as trilling and vibrato. They occur just on the edge of what can be followed directly. Finally, it is interesting to note that the lowest note on the piano is at 26.5 Hz, which is also in this range of problematic frequencies. However, the lowest note on the piano does not sound so clean. It is often described as "muddy" and is not often used. In fact, the note itself can almost be described as dissonant on its own!

To begin to understand how beats affects our perception of consonance and dissonance, let’s start with a pitch of A = 440 Hz and examine what happens when we play a second note. For example, if the second note is at 450 Hz, you will hear one pitch at the average frequency of 445 Hz, but you will also hear beats at 10 Hz. This will not sound dissonant. However, if the second note has a frequency of 480 Hz, the sound will seem harsh and unpleasant and this is what is referred to as dissonance. There is a beat frequency at 40 Hz, but you cannot hear that distinctly. It is also hard to tell if there are two notes being played.

If the second note is around 510 Hz, the beat frequency will be 70 Hz. At this point, you will still call the notes dissonant, but not as bad as the previous case. The two notes will now sound distinct and you can hear their individual pitches. Finally, for any frequency higher than about 530 Hz, the notes will be clearly distinct and consonant.

Now, how do these values compare to the intervals that we know? Well, a note a Just Major Third above 440 Hz has a frequency of 550 Hz. The analysis above says that this should sound consonant, which it does. So far, so good. However, this analysis would say that any pitch above a Major Third would sound consonant! For example, a seventh should sound consonant, although this is definitely a dissonant interval. Even the tritone, which is a half step less than a Perfect Fifth should sound consonant by this reasoning, although it is the most dissonant interval of all. So something must be missing from this analysis.

Back in Section 4.2, we discussed pure tones and complex tones. A pure tone consisted of a single frequency equal to the fundamental of the note. Musically, you almost never hear a pure tone, except for a tuning fork. Indeed, that is the purpose of a tuning fork. The problem is that you have no control over the quality of a pure tone, so it is musically not very interesting. Thus, all instruments produce complex tones: in addition to the fundamental frequency, the instrument also produces overtones and the number and loudness of the overtones determines the tone quality. Of course, for melodic instruments, the overtones are all harmonics and in this case, the pitch of the note is not changed by the presence of overtones.

But what is the connection with consonance and dissonance? The analysis we discussed applies only to pure tones. When we considered a note at 440 Hz, we assumed that that was the only frequency present. Or when we played 440 Hz and 550 Hz together, we assumed that there was only one beat frequency. In fact, the analysis is correct for pure tones. Two pure tones forming a tritone actually does not sound dissonant. So, while our analysis was correct, it just does not apply to musical tones, because musical tones never consist of a pure tone.

So, we must go back and rethink what happens when we play two complex tones together. When we say that we play a complex note with a pitch of 440 Hz, we must remember that we also have frequencies of 880 Hz, 1320 Hz, 1760 Hz, … present. Now, let’s add a second complex note at 600 Hz. Before, we would have said that this sounds consonant, since the beat frequency with 440 Hz is 160 Hz. But, just as with the first note, the second note contains frequencies at 1200 Hz, 1800 Hz, … Now, we must consider beat frequencies between all pairs of notes. So, we have 880-600 = 280 Hz, 1200-880 = 320 Hz, 1320-1200 = 120 Hz, and 1800-1760 = 40 Hz. Most of these beat frequencies are all right – if the beat frequency is relatively high, the brain is not concerned about it. However, the beat frequency at 40 Hz does cause a problem, as this is right in the range of the most dissonant beat frequencies. Thus, notes can sound dissonant not just because of the beat frequency between the fundamental frequencies of the notes, but because of beats between any pairs of overtones.

Because of the large number of overtones present in any complex tone and the greater number of pairs of overtones that must be considered, you might think that there are always going to be some dissonant beats frequencies. Basically, this is correct! Any two random complex notes will probably sound dissonant. But this is exactly why only special notes are used in a musical scale. Under certain conditions, the overtones of the pair of notes line up in such a way that there are no unpleasant beats.

For example, a again consider a pitch of 440 Hz and now let’s use the note a Perfect Fifth higher at 660 Hz. First, we need the harmonics of each note:

In this case, the harmonics are either widely spaced and have large beat frequencies (e.g. 1760 and 1980 Hz), or the harmonics are exactly the same (e.g. both have 1320 as a harmonic). Generally, overtones which are close in frequency produce dissonance, unless, they happen to be exactly the same. This is why two notes exactly a Perfect Fifth apart sound consonant, while if one note is slightly out of tune, the pair sounds very dissonant. For example, if you play the note at 660 Hz just 10 Hz too high, at 670 Hz, the second harmonic will be at 1340 Hz. This will beat with the harmonic at 1320 Hz in the first note with a frequency of 20 Hz, and this will sound very unpleasant! So, consonance and dissonance are really determined by the frequencies of the overtones of the two notes. We will discuss this more in Chapter 7.