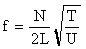So far, we have focused on the fact that waves repeat in time. The time it takes to repeat is called the period and the number of times it repeat in one second is called the frequency. However, if you ever sat at the ocean and watched water waves role in, you would realize that waves also repeat in space. So, a better definition of a wave is something that repeats in time and in space. The important quantity is then how far does it take for a wave to repeat in space. This distance is called a wavelength:

A wave repeats in time in one period. A wave repeats in space in one wavelength.

For example, again imagine you are at the beach watching the waves in the ocean. The time between when the waves break is the period of the wave and the distance between crests while the waves are out in the ocean is the wavelength.

This applies to waves on a string, as well. Look back at the last figure in Section 3.3. Those are all examples of waves in space on a string. What you should notice is that a wavelength is twice the distance between nodes. After one node, it looks like the wave is repeating, except that it is upside down. Only after two nodes is the wave really repeating.

Here is an example problem: I have a 1 meter length of string which vibrates at f_a = 500 Hz.

1. What is the wavelength of this mode, l_a?
2. I place a bridge 1/3 of the way from one end, so that only the long portion can vibrate. What is the frequency and wavelength of the new fundamental, f_b, l_b?
3. Now, I only use the bridge when I pluck the string. What is the frequency and wavelength now, f_c, l_c?
4. What is the interval between f_b and f_c?

Often we interchange space and time. If someone asks you how far is it from Storrs, CT to Boston, you might say 90 miles or an hour and a half. Both answers would be regarded as perfectly normal. What is needed to make this connection? A speed or a velocity.

To make the connection between the frequency and the wavelength of a wave, we also need a velocity: the velocity of the wave.

What is the velocity for sound waves? It is very fast, about 343 meters/second, or about 767 miles/hour.

The concept of a wave velocity simplifies things a lot, because it connects frequency and wavelength in very simple way:

frequency× wavelength = velocity. OR f× l = v

The wavelength is generally given the symbol l, the Greek letter for "L". Wavelength is a distance, so it is usually given in meters. As we know, f is the frequency and has units of Hz = 1/sec. So the product f× l has units of meters/sec, which, in fact, is a velocity. The symbol for velocity is "v".

How does all of this relate to a vibrating string. Remember, the frequency of a string is given by

,

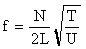where N is the mode of vibration of the string. The distance between nodes is L/N, so the wavelength is l = 2L/N. Let’s rewrite the equation a little differently:

,

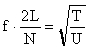so we can write

.

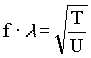Thus, we see that

.

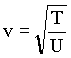For different waves, just need to know or measure the velocity of the wave. Then you can convert from wavelength to frequency and back. It is always true that f× l = v. The velocity depends on the details of the particular kind of wave. For example, the velocity of a wave on a string depends on the tension of the string, the density of the string, and the fact that you are considering strings, at all. The velocity of sound depends on various properties of air, and the fact that the wave moves through air.

The wavelength does not depend on the details of a vibrating system: it does not depend on the tension or the density for waves on a string. However it does depend on the geometry: the wavelength on a string does depend on the length of the string and the number of nodes.

Finally, we know that the distance between nodes is half a wavelength. So is the distance between antinodes. This means that the distance between a node and an antinode is a quarter of a wavelength, or l /4.