Section 2.1
a) What is the period of this wave?
b) What is the frequency of this wave?
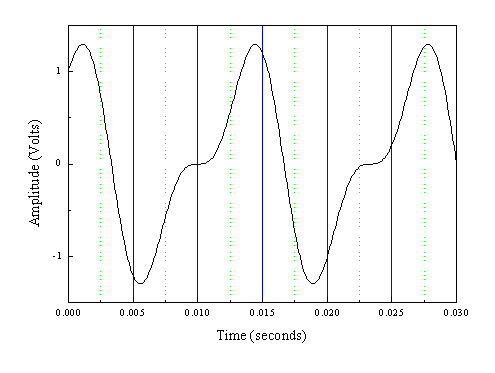
a) What is the period of this wave?
b) What is the frequency of this wave?
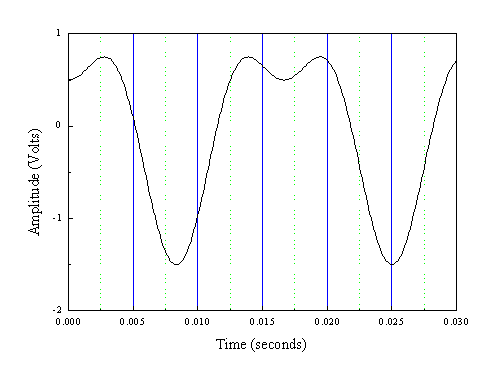
Before CDs people listened to records on a turntable. If the turntable revolved at 45 revolutions per minute, what is the period of this system in seconds? What is the frequency in Hz?
Section 2.2
a) Convert 55 miles/hour to ft/sec:
b) Convert 343 meters/sec to miles/hour:
Section 2.3
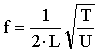 .
.a) If I increase the length, will the frequency increase or decrease?
b) If I increase the tension, will the frequency increase or decrease?
c) If I increase the string density, U, will the frequency increase or decrease?
d) If I change the length by a factor of 5, by what factor does the frequency change?
e) If I change the tension by a factor of 5, by what factor does the frequency change?
f) If I change the string density by a factor of 5, by what factor does the frequency change?
a) If you increase the density, U, of a string, the frequency will (increase | decrease | stay the same)?
b) What has a greater effect on the frequency of the string: Doubling the density or doubling the length?
c) Originally, the string has a frequency of 375 Hz. If I increase the tension by a factor of 2.4, what is the new frequency of the string?
Refer to the formula for a vibrating string in Section 2.2.
a) If I double the length of the string, will the frequency increase or decrease and by what factor?
b) If I decrease the density of the string by a factor of 16, will the frequency increase or decrease and by what factor?
c) If I increase the tension by a factor of 4, will the frequency increase or decrease and by what factor?
d) If I increase the tension by a factor of 3, by what factor should I change the density to keep the frequency the same?
e) If I decrease the density by a factor of 4, by what factor should I change the length to keep the frequency the same?
The frequency of the fundamental of a string is given by the formula:
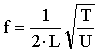 .
.I start with a frequency of 700 Hz. If I increase the tension by a factor of 4 and increase the density of the string by a factor of 9, what will be the new frequency?
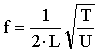 ,
,where L is the length of the string, T is the tension and U in the density.
a) If I double the length of the string, how will the frequency change?
b) If I increase the density of the string by a factor of 16, how will the frequency change?
c) If I increase the tension by a factor of 9, how will the frequency change?
d) If I increase the tension by a factor of 3, how should I change the density to keep the frequency the same?
e) If I increase the density by a factor of 4, how should I change the length to keep the frequency the same?
R is the distance from the Sun and Msun is the mass of the Sun.
a) If I decrease the distance, will the period increase or decrease?
b) If I increase the mass, will the period increase or decrease?
c) If I change the distance by a factor of 5, by what factor does the period change?
d) If I change the mass by a factor of 5, by what factor does the period change?
R is the distance from the Sun and Msun is the mass of the Sun.
a) If the Earth was twice its distance from the Sun how long would it take the Earth to circle the Sun?
b) If the Sun was three times as massive, how long would it take the Earth to circle the Sun?
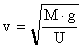 ,
,where M is the mass on the end of the string, g is the acceleration of gravity and U is the mass per unit length of the string. For a particular string, a mass of 1 kg gives a velocity of 100 m/sec. What mass would produce a velocity of 300 m/sec?
If the pressure is kept the same, what is the speed of sound in helium?
If the pressure is kept the same, what is the speed of sound in xenon?
A particular string gives a speed of 400 m/sec. If we want to increase the speed to 600 m/sec, by what factor should we change the density of the string, if we keep the tension the same?
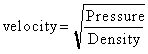 .
.We can change the density of air by changing its composition.
a) In normal air the speed of sound is 343 m/sec. If I increase the density of the air by a factor of 3, does the speed of sound increase or decrease? By what factor will it increase or decrease?
b) If I want to increase the speed by a factor of 4.5, how should I change the density of the air?
|
|
Length, L |
Frequency, f |
L*f |
|
f/L |
|
1 |
0.1 meter |
1.576 Hz |
|
|
|
|
2 |
0.3 meter |
0.910 Hz |
|
|
|
|
3 |
0.8 meter |
0.557 Hz |
|
|
|
|
4 |
1.2 meter |
0.455 Hz |
|
|
|
|
5 |
1.9 meter |
0.361 |
|
|
|
b) Graph the functions h(x) = x2/10 and k(x) =