As discussed in Chapter 1, one of the most difficult aspects of science is language. The language of science is initially a foreign language, as no one grows up from a small age speaking this language, making it difficult to learn. However, a precise language of science is critical to allow thousands and thousands of scientists to communicate with each across many different countries and cultures and across the ages. Ultimately, this textbook is a course in modern physics, but much of the early material concerns an ancient Greek scientist, Pythagoras. How is it that we can learn from Pythagoras? It is because he created a rational framework for describing and analyzing the natural world that is as valid today as it was 2000 years ago. This Pythagorean approach to the world has been so successful that we still use essentially the same approach today. Thus, understanding what Pythagoras did in ancient Greece will help us understand the endeavor of modern physics today.

As soon as we began to discuss various properties of sound waves in the last chapter, we started to introduce a new language. Part of this language is similar to our everyday language. Certain words are defined and given specific meanings, such as frequency. However, our scientific language included some new elements: units, graphs, and formulas. These elements are not used in everyday language and are less familiar. So, before we continue our discussion of waves, we must spend some time on these new elements.

When we introduced the concept of frequency, we used the example of the note A 440. This raised the question, 440 what? The "what" is the unit. In this case, there are 440 oscillations/second. Thus, the unit is oscillations/second, which is also referred to as the Hertz, or Hz for short.

Any quantity must have a unit to go along with it. It makes no sense to say that it is 90 to Boston. One can say that it is 90 miles to Boston and, so, here, the unit is a mile. The only issue related to units is that there are often many different units for the same physical quantity. For example, it may be 90 miles to Boston, but it is also 475,200 feet or 149 kilometers or 158,400 yards. The physical distance is the same, but how it is expressed can change. So, we must be able to convert from one unit to another.

The key to converting units is to always multiply the original quantity by 1. This will not change the physical value. The only difficult part is to figure out what form of 1 to use! For example, we might want to know how many seconds there are in 1 day. We know that 1 day is the same as 24 hours, so we can write: 1 = .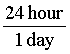

Also, 1 hour is equal to (60*60) seconds = 3600 seconds. So, 1 = .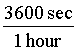

Finally, to convert 1 day into seconds, we have:

1 day*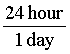* 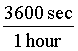= 86,400 sec. The important point is that the days and hours canceled out, leaving just seconds.

Graphs offer a way of presenting information to us that can make it easier to understand or extract information from a set of data. In fact, a graph can tell a whole story.

For example, a physicist works at a high-tech company and gets a raise of some amount each year. However, one year she makes a particularly important discovery and receives an extra raise. Here is her salary for each year. In which year did she make the big discovery?

The first thing that you will probably notice is that the years are out of order. This makes it very hard to read the table. Second, even with a calculator it would probably take you a awhile to figure out what year the big raise occurred. However, now try plotting the salary against the year - it will become immediately obvious when the jump in salary occurred!

For another example, the following graph shows my progress as I drove to Boston one day:

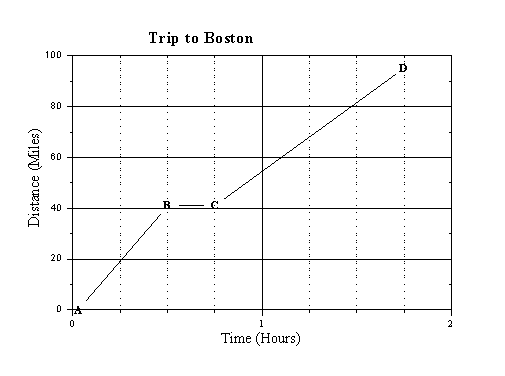
This graph tells a story - the goal is to explain what happened. At first, your explanations may seem contrived. But, when you figure it out, you really feel that you have the right answer. Actually, there are two good answers! Can you get them both?

Formulas or relationships are probably the hardest part of the language of science for non-scientists to use or appreciate. However, they are probably the most important result from scientific work. They really contain and summarize the information and knowledge that physicists produce. Moreover, the meaning and significance of formulas is never really taught to non-scientists, so we will spend quite a bit of time on them.

For example, the frequency at which a string can vibrate is given by the following formula: 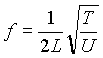. Or, another formula that you might remember from a High School science course that describes a gas in a container is: . If you are given the values of the various quantities in the formula, you can readily plug the numbers into a calculator and get a result. However, formulas actually contain much more information than this. For example, perhaps we don't know the value of all the quantities in a formula. In this case, you might think that the formula will be useless. On the contrary, it can still provide useful information, as we will see below.

In many physics courses, a lot of time is spent deriving formulas, which can often involve more advanced mathematics. The derivation of many formulas requires calculus, so we will not concern ourselves with derivations. This is not unreasonable: theoretical physicists devote their time to deriving formulas, and, often, I cannot even understand the mathematical methods that they use. But this is not a problem, as long as I can both understand how to use the formula and test it to make sure that it is correct. A physicist can use very fancy mathematics, but if the formula does not work in an experiment, it must be wrong. In this course, you will need to know how to work with formulas and you will test every one that we use in a lab.

There are 4 steps to fully understanding a formula. We will illustrate these steps with the formula for a gas in a container mentioned above.

The question is the following: what is the pressure of the gas in a container.

We will discuss the next two steps in the next section.