PHYSICS OF MUSIC - REVIEW SHEET #1

*Dependencies:

For example, the velocity of a wave on a string is:

If I double the tension, how does the velocity change?

*Unit conversion:

Must be able to convert from one type of unit to another.

*Intervals:

Perfect - Unison, Octave, Fifth, Fourth.

Pythagorean - all based on fourths and fifths.

Just - all intervals are kept simple, e.g. major third = 5/4.

Equal temperament (piano) - half step = 1.0595.

*Pythagorean scales:

Generation - create by going up and down by fifths and octaves.

Pentatonic - five note scale.

Diatonic - seven note scale.

*Oscillations:

Pitch/frequency - oscillations/sec.

Period - time for one oscillation.

Amplitude - loudness.

Shape or waveform - gives tone quality.

*Frequency of oscillation:

Fundamental - the lowest frequency at which a system can vibrate.

Overtones - all frequencies (including the fundamental) at which a system can vibrate.

Harmonics - integer multiples of the fundamental.

Complete harmonic series - a series of frequencies which has only and all harmonics.

Incomplete harmonic series - a series of frequencies which has only, but not all harmonics.

Medium - material which supports the wave.

Wave - disturbance in the medium.

Restoring force - force which returns medium to an equilibrium state.

*Wavelength - l, the distance at which a wave starts to repeat.

*Nodes - positions where a wave is stationary. Distance between nodes = l/2.

*Antinodes - positions where a wave is a maximum. Distance between a node and an antinode = l/4.

*Boundary conditions - tells you if there is a node or an antinode at the boundary of a cavity.

Wave velocity - waves travel a fixed speed,

*Wave equation: f× l = v.

Longitudinal - displacement in the same direction that the wave propagates.

Transverse - displacement perpendicular to the direct that the wave propagates.

Standing wave - a wave where the positions of the nodes and antinodes do not move.

Traveling wave - a freely propagating wave.

*Strings:

Frequency - inversely proportional to the length, .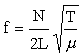

Restoring force - Tension.

Wave velocity -

Overtones - same as the harmonics.

Boundary conditions - nodes at each end.

*Restoring force - Pressure.

Wave velocity -

*Closed end - must have an antinode.

*Open end - must have a node.

Restoring force for surface waves - surface tension.

Surface wave velocity -

Boundary conditions - antinodes at boundaries.

*Bars (Metal, Wood):

Overtone series - not harmonic.

Fundamental - depends inversely on the square of the length of the bar.

*Waves in 2-D - Sound waves:

Regular series - simple frequencies as for an air column in both directions.

Combination tones - any combination of frequencies from the regular series added according to the Pythagorean Theorem- a² + b² = c².

Nodal lines - lines on which the wave is stationary.

*Additive - if two waves exist at the same place at the same time, their amplitudes must be added together.

*In phase - the peaks of the two waves match up, as do the troughs.

*Out of phase - the peaks of one wave line up with the troughs of the other wave.

*Constructive interference - the sum of the two waves is bigger than either wave, occurs when the waves are in phase.

*Destructive interference - the two waves cancel each other out, occurs when the two waves are out of phase.

Interference pattern - a description of the points in space where the two waves add constructively and destructively. To determine whether two waves will interfere constructively or destructively at a specific point, one must calculate the distance from the point to the sources of the two waves, labeled R₁ and R₂. If the difference R₂ - R₁ is zero or an integer multiple of a wavelength, the waves will be in phase and interfere constructively. If the difference R₂ - R₁ is a half of a wavelength, the waves will be out of phase and interfere destructively.

Beats - the result of the interference of two waves which have different frequencies and wavelengths. At certain times, the waves will be in phase and add constructively. At a later time, the waves will be out of phase and add destructively. This oscillation between constructive and destructive interference will occur with a frequency equal to the beat frequency, which is given by the difference between the two original frequencies.