Laboratory #5: Sound Waves in a Rectangular Cavity

Objective:

So far, we have only considered waves in one dimension. Waves in two dimensions are quite common (like the head of a drum). In this experiment, we will find the resonant modes of a thin rectangular cavity. This is pretty close to a two dimensional system and the pattern of overtones can be quite complex. We will measure the resonant frequencies, as in Lab 3, but this time, we will use a more sophisticated technique. The results can be obtained more rapidly and more accurately, allowing us to perform a much better analysis. In this experiment, we will play a sound file that sweeps in frequency from 0 Hz to 5,000 Hz, at a rate of 200 Hz/sec. While this is playing, the PASCO software will record the amplitude of the signal from the microphone. This will trace out all of the resonances of the cavity. To find the resonances, you will simply need to place the cursor at the peaks and record the values. Remember:

frequency× wavelength = velocity.

Equipment:

  1. Computer and PASCO software with LAB5.
  2. Speaker and microphone.
  3. Amplifier in REC setting.
  4. Plastic L’s to form a rectangular cavity with the long dimension between 17-20 cm.
  5. Top and bottom plates. Microphone in bottom plate.
  6. Ruler.

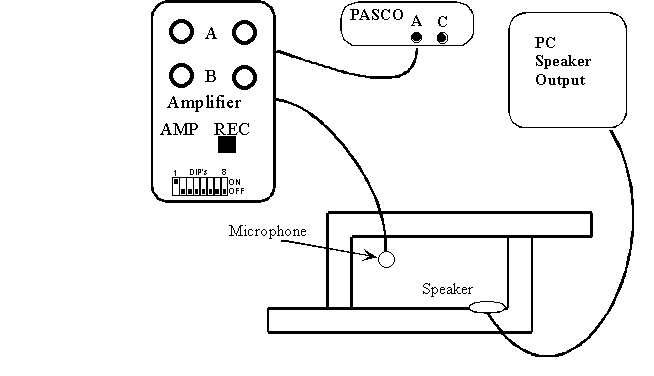
Diagram:

Instructions:

  1. Start up PASCO software and open the file Lab5.sws.

  2. Open the Sound Player and open file Lab5.wav.

  3. Measure the two sides of the rectangle and calculate all combinations of resonant frequencies up to 5000 Hz.

  4. To record the data, you click the record button in the PASCO window and then start the wave file. The PASCO program will not start recording until the wavefile starts. It will stop recording when the wavefile ends.

  5. With the cursor, record the time of each peak. To convert to frequency multiply by 200 Hz/sec. If the peaks are large in amplitude and do not have a sharp peak, repeat the scan at a lower volume because the peaks are saturated.

DATA:

EXPECTED FREQUENCIES:

Use v = 343 m/sec.

f = (n× v)/(2× L)

Length 1 (meters)

Length 2 (meters)

    

Frequency 1 (Hz)

Frequency 2 (Hz)

Combination Frequency (Hz)

  
       
       
       
       
       
       
       
       
       
       

 

MEASURED FREQUENCIES:

Time of Peak (sec)

Measured

Frequency (Hz)

Expected

Frequency (Hz)

Ratio:

Measured/Expected
       
       
       
       
       
       
       
       
       
       
       
       
       
       
       

 

Questions:

  1. How well did your estimates match the measured values? Find the average of the ratio of the expected to the measured values.

 

 

 

 

 

 

 

 

  1. This ratio is a measure of how far off your value of the speed of sound was. What is your measured speed of sound? If fact, the speed of sound is approximately given by:

Speed of sound = (331.3 + 0.6T) m/sec

where T is the temperature in ° C

See if your measured speed of sound agrees with this by measuring temperature in the room.