Laboratory #3: Sound Waves in a Tube

Objective:

In Lab #2 we found the conditions to excite various modes of a string and found the relationship between the resonant frequency and the mass and tension of the string. In this lab, we will make a similar measurement for sound waves in a tube. Here, the task is more difficult because we cannot SEE the waves, themselves. This is usually the case in physics. Since we cannot see the amplitude of the waves, we will have to measure them in a different way. Remember:

frequency× wavelength = velocity.

We will also study the "end correction" for an air column. If an air column has an open end, there should be a pressure node at that end. However, the node actually is a little past the end of the tube, by an amount

End correction = 0.6× (radius of tube).

This makes the tube effectively longer.

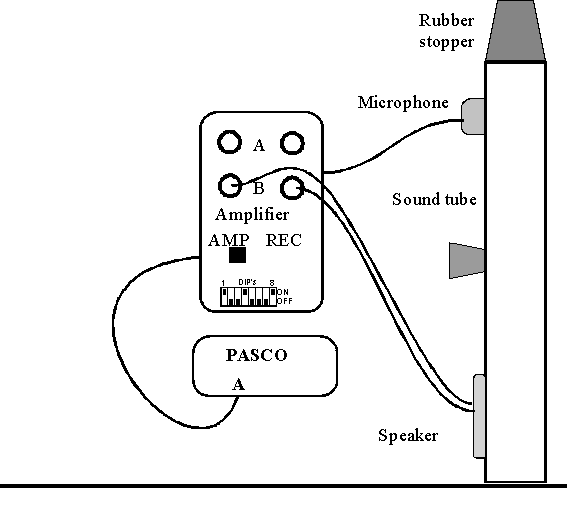
Equipment:

  1. Computer and PASCO software.
  2. Speaker, microphone, amplifier in AMP setting.
  3. Cylindrical plastic tube with one stopper.
  4. Ruler.

Set-Up:

Instructions:
  1. Start up PASCO software and set the x-axis range on the spectrum analyzer to 3000 Hz.
  2. Start the PASCO function generator with a sine wave at about 0.1 V and a frequency of 500 Hz.
  3. Find the first 4 resonances for the closed-closed tube. Stand tube on end and place wide end of stopper on the tube. Increase voltage as necessary up to 0.5 V.
  4. Scan in steps of 100 Hz to find a resonance, then scan by 10 Hz, and finally 1 Hz to get an accurate value. (Look in notepad for shortcuts). Rescale the y-axis as necessary.
  5. Repeat this for the open-closed tube (i.e. remove the stopper) and the open-open tube (just lay tube on table).
  6. Measure the physical length of the air column for the closed-closed tube.

DATA:

Physical tube length = .

Closed-Closed

Tube

Frequency
(Hz)

Wavelength
(m)

Speed of
Sound (m/sec)

1

      

2

      

3

      

4

      

Average speed of sound (using n=3 and n=4) =

Open-Closed

Tube

Frequency
(Hz)

Wavelength
(m)

Effective tube
length (m)

1

      

2

      

3

      

4

      

Average effective tube length = End correction =

Open-Open

Tube

Frequency
(Hz)

Wavelength
(m)

Effective tube
length (m)

1

      

2

      

3

      

4

      

Average effective tube length = End correction per end =

Questions:

1) Speed of sound

a) For each measurement of the closed-closed cylindrical tube calculate the wavelength of the mode using ln = 2L/n. Then calculate the speed of sound for each frequency using: speed of sound = frequency× wavelength.

 

 

 

 

b) Average the results for the speed of sound for n=3 and 4. How close (in percent) is this value to the known speed of sound?

 

 

 

 

2) Effective length of the tube.

a) For the open-closed tube and the open-open tube calculate the wavelength corresponding to each frequency using: wavelength = (speed of sound)/frequency. Use the speed of sound from the results of question 1).

 

 

 

 

b) Using the wavelengths from 2a, determine the effective length of the tube for the open-closed and open-open cases. Remember ln = 2L/n for an open-open tube and ln = 4L/(2n-1) for an open-closed tube.

 

 

 

 

c) Finally, the end correction is the effective tube length minus the physical tube length. (Note, the open-closed has one end correction, the open-open has two). What is the measured end correction per open end and how well does this agree with the formula for the end correction?