
Laboratory #2: Vibrating String
Objectives:
Equipment:
Setup:

From class we know that:
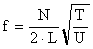 ,
,
where T = Mg is the tension, U is the mass of a one meter length of string, L is the length of the string, N is the overtone number and g = 9.8 m/sec2. So,
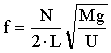 .
.
Instructions:
Part A
Results:
Table 1
String length =
|
|
Mass, M |
Fundamental, f1 |
Second harmonic |
Third Harmonic |
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
Table 2
Mass =
|
|
Length, L |
Fundamental, f1 |
Second harmonic |
Third Harmonic |
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
Analysis:
Consider four possible dependencies:
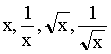 .
.
We want to see which one works for our data. For each table, fill in the values and circle the column which gives a constant value.
First, check the fundamental frequency, f1 vs. M, from Table 1:
|
f |
M |
f× M |
f/M |
f× Ö M |
f/Ö M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Now, check f1 vs. L, from Table 2:
|
f |
L |
f× L |
f/L |
f× Ö L |
f/Ö L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Finally, check f vs. N for any one row from Table 1 or 2:
|
f |
N |
f× N |
f/N |
f× Ö N |
f/Ö N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Questions: